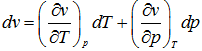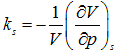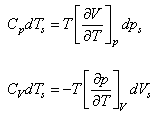Some definitions

In a single phase region, where pressure and temperature are independent, we can think of the volume as being a function of pressure and temperature.

V = V (T, p)

1.146

or,

v = v(T, p)

1.147

Applying the chain rule of the calculus

1.148

The derivative 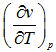represents the slope of a line of constant pressure on V - T a plane. A similar interpretation can be given for the second derivative. These derivatives are themselves intensive thermodynamic properties, since they have definite values at any fixed thermodynamic state. The first represents the sensitivity of the specific volume changes in temperature at constant pressure, and the second is a measure of the change in specific volume associated with a change in pressure at constant temperature. Isothermal compressibility, isentropic compressibility and volume expansivity are defined as

Isothermal compressibility: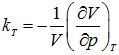

Volume expansivity: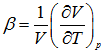

The compressibility factors are frequently tabulated functions of state. The “co-efficient of linear expansion” used in elementary strength of materials texts is

3β Young's modulus of elasticity is proportional to k_T in terms of β and k_T, Eq. (1.148) can be written as

dv = β vdT - kT vdp

1.149

Usefulness of Eq. 1.149 arises from the fact that β and k_T are sometimes slowly varying functions of T and P. Another term in use is the isothermal compressibility defined as

1.150

1.151

Based on the definitions of isothermal compressibility and volume expansivity, the specific heat differences can be written as

Ratio of heat capacities

At constant entropy S , the two T - dS relations become

1.152   1.153

Dividing Eq. (1.152) by Eq. (1.153) and using Theorem 3

1.154