Exercises:

1. Prove lemma (40.1)
2. Show that the Prüfer group (40.3) is the inductive limit of the sequence of multiplicative cyclic groups 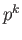$C_{p^k}$ of order 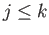$p^k$, where $p$ is a prime number.
3. Discuss the existence of inductive limits of directed systems in the categories Gr and Top.
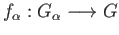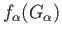4. Suppose that $\{G_{\alpha}/\alpha\in \Lambda\}$ is a directed system of groups with inductive limit $G$ and associated maps $f_{\alpha}:G_{\alpha}\longrightarrow G$, show that $G$ is the set theoretic union of the images $f_{\alpha}(G_{\alpha})$, $\alpha \in \Lambda$.

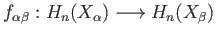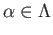in

Lecture - XLI The Jordan-Brouwer separation theorem

in We conclude the course with a proof of the Jordan Brouwer theorem, a far reaching generalization of the Jordan curve theorem (theorem 1.1). The most transparent and clear proof of the Jordan Brouwer theorem uses the notion of inductive limits developed in the previous lecture. We shall follow closely the treatment in [16] demonstrating the power of the Mayer Vietoris sequence.