The fact that
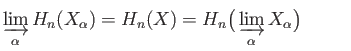 is an inductive system is clear. Let
is an inductive system is clear. Let
 denote the inductive limit of this system in AbGr and
denote the inductive limit of this system in AbGr and
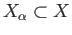 denote the
associated homomorphisms described in definition (40.2). The
inclusion maps
denote the
associated homomorphisms described in definition (40.2). The
inclusion maps
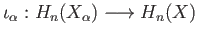 induce homomorphisms
induce homomorphisms
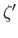 . To simplify notations, we shall
suppress the bar and
use the same symbol
. To simplify notations, we shall
suppress the bar and
use the same symbol 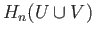 to denote a cycle as well as the homology class it represents.
The proof of (41.1) hinges on two simple facts:
to denote a cycle as well as the homology class it represents.
The proof of (41.1) hinges on two simple facts:
- (i)
- If
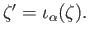 is an
is an  chain in
chain in  then there exists an
then there exists an
 such that the images of the
constituent simplicies in
such that the images of the
constituent simplicies in
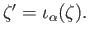 are all contained in
are all contained in
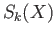 . We shall say that the chain
. We shall say that the chain
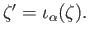 is supported in
is supported in
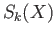 .
Thus
.
Thus
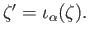 may be viewed as a singular
chain in
may be viewed as a singular
chain in
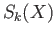 and the latter will be provisionally denoted by
and the latter will be provisionally denoted by 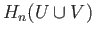 in the proof.
Further if
in the proof.
Further if
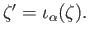 is a cycle in
is a cycle in  then
then
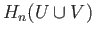 is a cycle in
is a cycle in
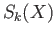 and
and
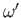
- (ii)
- If
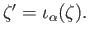 is a boundary of a chain
is a boundary of a chain
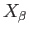 in
in  then there exists a
then there exists a
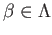 such that
such that
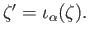 and
and
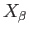 are both supported in
are both supported in 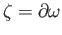 and the relation
and the relation
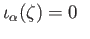 holds in
holds in
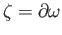 . In other words,
. In other words,
To prove these note that the image of each singular simplex is a compact subset of  and each chain is a finite
linear combination of singular simplicies.
and each chain is a finite
linear combination of singular simplicies.
Property (2) of definition (40.2) may now be applied
to the family of homomorphisms
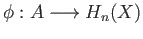 . There exists a group homomorphism
. There exists a group homomorphism
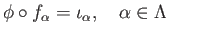 such that
such that
To show that  is surjective, by (i) above, an arbitrary
cycle
is surjective, by (i) above, an arbitrary
cycle
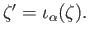 in
in  with support in
with support in
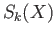 representing an element of
representing an element of 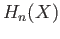 may be expressed as
may be expressed as
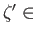 where
where
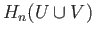 is a cycle in
is a cycle in
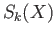 . By (41.3) we see that
. By (41.3) we see that
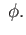 im
im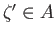 To show that
To show that  is injective, let
is injective, let
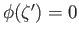 be such that
be such that
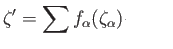 in
in  . By exercise 4 of lecture 40, we can write
. By exercise 4 of lecture 40, we can write
where the sum is finite and each
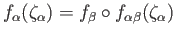 is a cycle in
is a cycle in
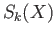 . Choose a
. Choose a 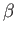 exceeding all the
indices in (41.4) and for each index
exceeding all the
indices in (41.4) and for each index 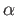 in (41.4),
in (41.4),
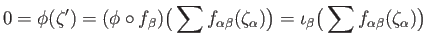 and so using (41.3),
and so using (41.3),
Invoking (41.2) we arrive at
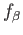 (perhaps with a larger
(perhaps with a larger 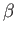 ).
Applying
).
Applying 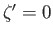 we see that
we see that
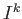 as desired.
as desired.  nisha
2012-03-20
nisha
2012-03-20
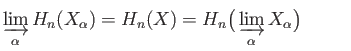 is an inductive system is clear. Let
is an inductive system is clear. Let
![]() . There exists a group homomorphism
. There exists a group homomorphism
![]() such that
such that