Let  be a topological space and
be a topological space and
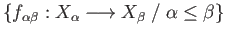 be a directed system of open
subsets of
be a directed system of open
subsets of  such that every compact subset of
such that every compact subset of  lies in some
lies in some
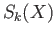 .
For a pair of indices
.
For a pair of indices
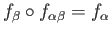 , the map
, the map
 is the homomorphism induced by inclusion
is the homomorphism induced by inclusion
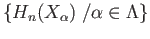 . Then,
the family
. Then,
the family
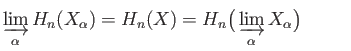 together with the maps
together with the maps
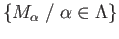 forms an inductive system of abelian groups and
forms an inductive system of abelian groups and
nisha
2012-03-20
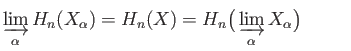 together with the maps
together with the maps