If 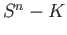 then
then  is a point and
is a point and 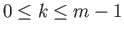 is homeomorphic to
is homeomorphic to
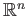 and
the result is true in this case. The proof now proceeds by induction on
and
the result is true in this case. The proof now proceeds by induction on 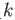 . Assume that the
result has been proved for
. Assume that the
result has been proved for
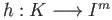 and let
and let
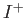 be a homeomorphism. Define the
halves
be a homeomorphism. Define the
halves 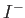 and
and 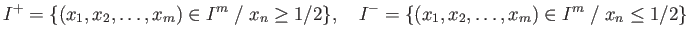 as
as
and note that
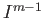 is homeomorphic to the cube
is homeomorphic to the cube 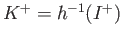 . We construct the sets
. We construct the sets
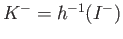 and
and
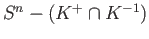 , and use the Mayer Vietoris sequence to the
following open cover
of
, and use the Mayer Vietoris sequence to the
following open cover
of
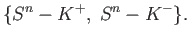 :
:
Since
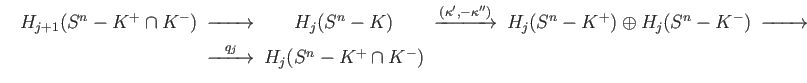 is homeomorphic to
is homeomorphic to 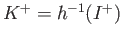 , by induction hypothesis the end terms of the portion
, by induction hypothesis the end terms of the portion
are zero if 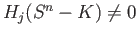 whereas the left most group is zero if
whereas the left most group is zero if 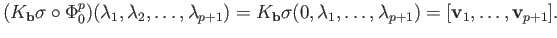 . In any case
. In any case
 is injective.
Assume that for some
is injective.
Assume that for some 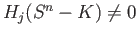 ,
,
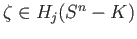 . We choose
. We choose
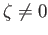 ,
,
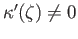 and
it follows
and
it follows
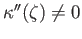 or
or
 . Let us assume
that
. Let us assume
that
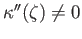 . Since
. Since 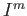 is homeomorphic to
is homeomorphic to 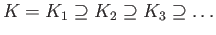 , the process can be repeated
subdividing
, the process can be repeated
subdividing 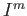 into two pieces whose intersection is homeomorphic to
into two pieces whose intersection is homeomorphic to 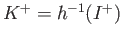 . Thus we construct a
nested sequence of subsets
. Thus we construct a
nested sequence of subsets
such that for each  ,
the map
,
the map
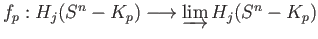 induced by inclusion, maps
induced by inclusion, maps 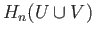 to a non zero element.
Composing with
to a non zero element.
Composing with
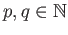 one checks that
for
one checks that
for
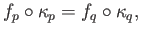 ,
,
thereby providing a map
Since the intersection
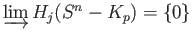 is homeomorphic to
is homeomorphic to 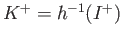 , by induction hypothesis,
, by induction hypothesis,
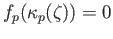 . Hence
. Hence
 for every
for every  and hence by theorem (40.2) (ii),
for some
and hence by theorem (40.2) (ii),
for some
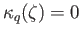 ,
,
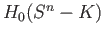 which is a contradiction.
which is a contradiction.
Turning to the case 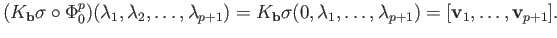 , assume that rank of
, assume that rank of
 is atleast two. If we select points
is atleast two. If we select points  and
and 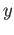 lying in distinct path components of
lying in distinct path components of 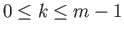 , the cycle
, the cycle
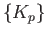 in
in 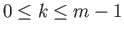 is not a boundary.
As before we construct a nested sequence of compact sets
is not a boundary.
As before we construct a nested sequence of compact sets 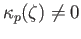 with
with
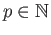 for each
for each
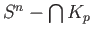 . But since
. But since
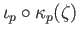 has only one path component,
has only one path component,
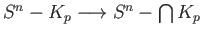 is a boundary where
is a boundary where 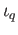 is the map induced by the inclusion
is the map induced by the inclusion
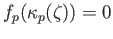 whence
whence
by (41.3). This in turn forces
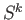 by theorem (40.2) (ii) and we have a contradiction.
nisha
2012-03-20
by theorem (40.2) (ii) and we have a contradiction.
nisha
2012-03-20
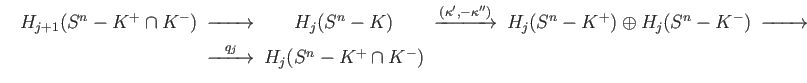 is homeomorphic to
is homeomorphic to ![]() , assume that rank of
, assume that rank of
![]() is atleast two. If we select points
is atleast two. If we select points ![]() and
and ![]() lying in distinct path components of
lying in distinct path components of ![]() , the cycle
, the cycle
![]() in
in ![]() is not a boundary.
As before we construct a nested sequence of compact sets
is not a boundary.
As before we construct a nested sequence of compact sets ![]() with
with
![]() for each
for each
![]() . But since
. But since
![]() has only one path component,
has only one path component,
![]() is a boundary where
is a boundary where ![]() is the map induced by the inclusion
is the map induced by the inclusion
![]() whence
whence