Let 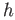 be the homeomorphism between
be the homeomorphism between  and
and  and
and 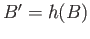 . We have to show that
. We have to show that
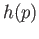 is an interior point of
is an interior point of  . Let
. Let  be a closed ball centered at
be a closed ball centered at  and contained in
and contained in  so that
so that
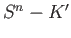 is a
compact subset of
is a
compact subset of  containing
containing 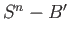 . Let
. Let 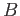 be the (topological) boundary of
be the (topological) boundary of  and
and
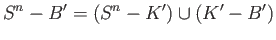 . We regard
. We regard  and
and  as subsets of
as subsets of  .
By theorem (41.2),
.
By theorem (41.2),
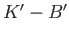 is path connected and
is path connected and
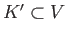 has two path components. However since the union
has two path components. However since the union
is a disjoint union of connected sets, the pieces
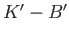 and
are the components
of
and
are the components
of
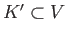 . Hence they are both open in
. Hence they are both open in
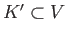 (why?)
and hence are open in
(why?)
and hence are open in  . The piece
is then an open subset of
. The piece
is then an open subset of  containing
containing 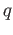 and since
we see that
and since
we see that
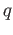 is an interior point of
is an interior point of  .
. 
nisha
2012-03-20