The result is clear if 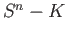 . We proceed by induction on
. We proceed by induction on 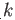 and assume the result with
and assume the result with
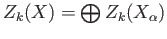 in place of
in place of 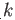 . Let
. Let
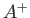 where
where 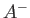 and
and 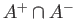 are each homeomorphic to
are each homeomorphic to 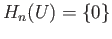 and
and
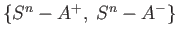 is homeomorphic to
is homeomorphic to 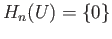 . The
Mayer Vietoris sequence may be applied to the open
cover
. The
Mayer Vietoris sequence may be applied to the open
cover
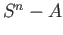 of
of 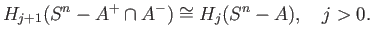 and the reader ought to verify that
and the reader ought to verify that
By induction hypothesis we get (41.5) for the case 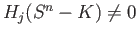 . Let us now consider the case
. Let us now consider the case 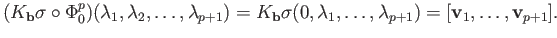 . The tail end of the
Mayer Vietoris sequence gives
. The tail end of the
Mayer Vietoris sequence gives
img
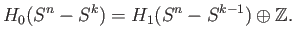
Since the image of 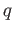 is isomorphic to
is isomorphic to
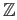 , we see that the kernel of
, we see that the kernel of 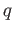 must also be isomorphic to
must also be isomorphic to
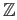 giving a short exact sequence
giving a short exact sequence
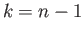
img
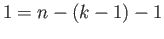
Since the image of 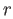 is free of rank one, (41.6) splits and we have
is free of rank one, (41.6) splits and we have
If 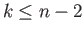 then
then
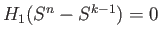 and so the induction hypothesis gives
and so the induction hypothesis gives
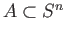 whereas if
whereas if
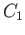 then
then
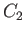 .
.  nisha
2012-03-20
nisha
2012-03-20