- Show that the map defined by (34.1) is the restriction to
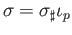 of an affine map. Note: An affine map
is the composition of a linear map and a translation.
of an affine map. Note: An affine map
is the composition of a linear map and a translation.
- Suppose
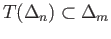 is an affine map such that
is an affine map such that
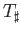 , then
, then
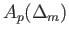 maps the subgroup
maps the subgroup
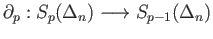 into
into
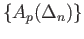 and is a chain map from the complex
and is a chain map from the complex
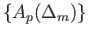 to
to
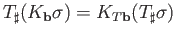 . Further prove the following:
. Further prove the following:
- (i)
- If
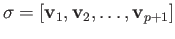 and
and
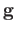 then
then
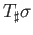 .
.
- (ii)
- If
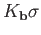 is the barycenter of
is the barycenter of  then
then 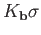 is the barycenter of
is the barycenter of
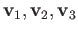 .
.
What happens if we consider a degenerate two simplex where the points
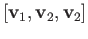 are not
affinely independent? Discuss the case of the two simplex
are not
affinely independent? Discuss the case of the two simplex
![$ [{\bf v}_1, {\bf v}_2, {\bf v}_2]$](img2752.png) .
.
- Examine what happens if the term referred to as junk in equation (34.7) is retained.
- Complete the details of the proof of theorem (34.4).
- Show that
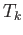 is chain homotopic to the identity map. What is the chain homotopy?
is chain homotopic to the identity map. What is the chain homotopy?
- Suppose that the maps
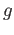 and
and 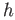 in the exact sequence
in the exact sequence
are replaced by the composites
the result is again an exact sequence.
- Fill in the details in the proof of theorem (34.8). See exercise 6 of lecture 29.
in
Lecture - XXXV The Mayer Vietoris sequence and its applications
in
The proof of Mayer Vietoris sequence is reminiscent of the Seifert Van Kampen theorem.
While the Seifert Van Kampen theorem enables us to relate the fundamental group of a union 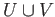 in terms of
the fundamental groups of
in terms of
the fundamental groups of 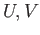 and
and 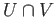 , the situation here is slightly more involved.
The precise relationship between the homologies of
, the situation here is slightly more involved.
The precise relationship between the homologies of
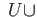 and
and 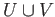 is described in terms of the long exact
sequence of theorem (34.7).
is described in terms of the long exact
sequence of theorem (34.7).
As in the Seifert Van Kampen theorem we obtain from a push-out diagram of topological spaces a push out diagram of
chain complexes which turns into a short exact sequence of complexes. The corresponding long-exact sequence gives, after
an application of the excision theorem of the last lecture,
the Mayer Vietoris sequence. It is one of the most efficient tools available for the computation of homology groups.
We restate here the theorem for convenience.
Subsections
nisha
2012-03-20