The first part follows from the fact that the homology groups 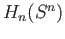 and
and 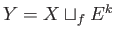 are
non-isomorphic. If
are
non-isomorphic. If
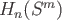 and
and
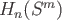 were homeomorphic then their one-point compactifications would also
be homeomorphic which means
were homeomorphic then their one-point compactifications would also
be homeomorphic which means  and
and 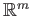 would be homeomorphic leading to a contradiction.
would be homeomorphic leading to a contradiction.
nisha
2012-03-20