We shall now consider the space
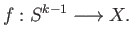 obtained by attaching a
obtained by attaching a 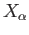 cell
cell 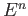 to
to  via an attaching map
via an attaching map
We shall closely follow the method used in lecture 26 to compute the fundamental groups of the projective plane
and Klein's bottle. We do not have to keep track of base points and
use the Mayer Vietoris sequence instead of the Seifert Van Kampen theorem.
We shall use the same notations
and denote by  the center of
the center of 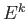 , the interior of
, the interior of 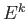 by
by  and the space
and the space 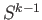 by
by  . The space
. The space
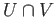 deformation retracts to a space homeomorphic to
deformation retracts to a space homeomorphic to 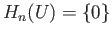 . Since
. Since  deformation retracts to
deformation retracts to  ,
the spaces
,
the spaces  and
and  have the same homology groups and
have the same homology groups and
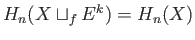 when
when 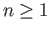 .
in
We are ready to prove the following result:
.
in
We are ready to prove the following result:
nisha
2012-03-20