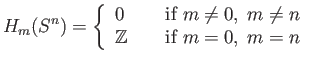We use equation
(29.18) to describe explicitly the
connecting homomorphism in the Mayer Vietoris sequence. Take a representative cycle 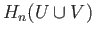 in
in
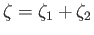 .
Theorem (34.6) implies that an arbitrary element of
.
Theorem (34.6) implies that an arbitrary element of
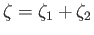 can be represented as a sum
of chains
can be represented as a sum
of chains
where
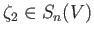 and
and
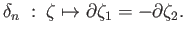 . Note that we are resorting to an
abuse notation in writing
. Note that we are resorting to an
abuse notation in writing 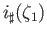 instead of
instead of
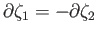 .
We conclude that
.
We conclude that
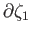 . Thus
. Thus
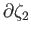 and
and
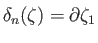 are both cycles in
are both cycles in 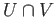 .
According to (29.18), the homomorphism
.
According to (29.18), the homomorphism 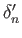 is given by
is given by
nisha
2012-03-20