Looking at the portion of the Mayer Vietoris sequence
we get the result directly when 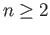 . If
. If 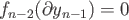 then
necessarily
then
necessarily 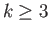 and we look at the portion of the Mayer Vietoris sequence
and we look at the portion of the Mayer Vietoris sequence
Observe that
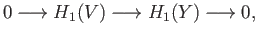 and we get the exact sequence
and we get the exact sequence
establishing the result when 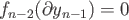 .
. 
The cases
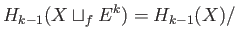 are more technical and we shall merely state the relevant results.
are more technical and we shall merely state the relevant results.
nisha
2012-03-20
![]() are more technical and we shall merely state the relevant results.
are more technical and we shall merely state the relevant results.