We take
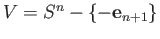 and
and
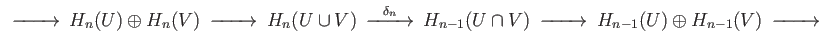
and note that 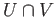 deformation retracts to
deformation retracts to  . Consider the portion of the Mayer Vietoris sequence
. Consider the portion of the Mayer Vietoris sequence
Since 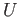 and
and 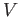 are contractible spaces, we get for the case
are contractible spaces, we get for the case 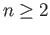 ,
,
and hence
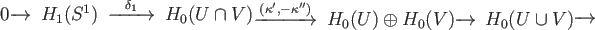 (
(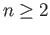 ).
).
By induction the result would follow as soon as we prove it for the case 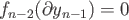 .
.
For this case let us take a look at the
end of the Mayer Vietoris sequence:
Since 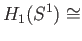 is injective,
is injective,
To understand the map
 we take a basis of
we take a basis of
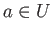 consisting of a pair of points
consisting of a pair of points
 and
and 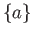 .
.
The singleton 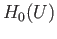 generates
generates 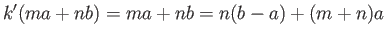 and
and
which is a boundary in 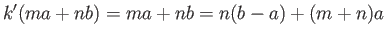 if and only if
if and only if 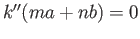 .
.
Likewise
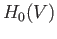 in
in 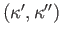 if and only if
if and only if 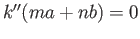 . Thus the kernel of
. Thus the kernel of
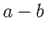 is the infinite
cyclic group
is the infinite
cyclic group
generated by the zero chain 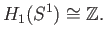 . Hence we get
. Hence we get
To calculate 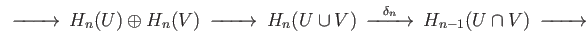
for 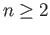
we look at the portion of the Mayer Vietoris sequence
and observe that since
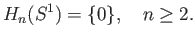 when
when 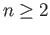 ,
,
nisha
2012-03-20