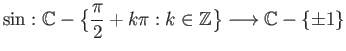- Suppose that
 and
and
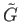 are topological groups and
are topological groups and
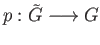 is a covering projection that is also a group
homomorphism then
ker
is a covering projection that is also a group
homomorphism then
ker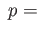 Deck
Deck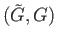 .
.
- Determine the deck transformations for the covering
- Determine the deck transformations for the covering
given by
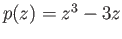 . Show that this covering is not regular. Hint: Use Riemann's removable singularities
theorem to show that a deck transformation must be analytic on the whole plane.
. Show that this covering is not regular. Hint: Use Riemann's removable singularities
theorem to show that a deck transformation must be analytic on the whole plane.
- If
 is a prime, what can you say about the group of deck transformations of a
is a prime, what can you say about the group of deck transformations of a  -sheeted covering space?
-sheeted covering space?
- Show using the universal property that the universal covering, if it exists is unique upto isomorphism of
covering projections.
in
Lecture XX - Orbit Spaces
Many interesting spaces in geometry arise as the space of orbits under the action of groups. We have seen examples of this already in lecture 4.
An important special case is when the group action is discrete such as the case of the multiplicative group 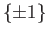 on the sphere
on the sphere  resulting in
the real projective space
resulting in
the real projective space
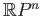 .
.
Subsections
nisha
2012-03-20