Let
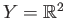 and
and  be the group generated by the
affine maps
be the group generated by the
affine maps 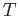 and
and 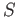 given by
given by
Note that 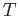 and
and 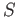 are isometies and the group generated by these acts properly discontinuously on
are isometies and the group generated by these acts properly discontinuously on
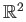 .
The
orbit space is the Klein's bottle
.
The
orbit space is the Klein's bottle  . Thus
. Thus
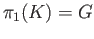 .
Now
.
Now
The fundamental group of the Klein's bottle is non-abelian. Note that
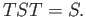 There are no other independent relations and the fundamental group of the
Klein's bottle is the group on two generators
There are no other independent relations and the fundamental group of the
Klein's bottle is the group on two generators
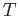 and
and 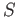 with one relation
with one relation 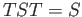 . Summarizing we have
. Summarizing we have
nisha
2012-03-20