Consider the strip
![$ Y = [0, 1]\times \mathbb{R}$](img1662.png) and let
and let
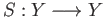 be the homeomorphism
be the homeomorphism
of  . Then
. Then 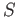 generates an infinite cyclic group of homeomorphisms of
generates an infinite cyclic group of homeomorphisms of  acting properly discontinuously on
acting properly discontinuously on  . The resulting orbit space
is the Möbius band. It is an exercise to show that the cylinder is a double cover of the Möbius band.
. The resulting orbit space
is the Möbius band. It is an exercise to show that the cylinder is a double cover of the Möbius band.
nisha
2012-03-20