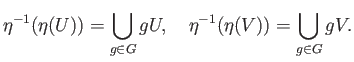Pick distinct points
 and let
and let  and
and  be disjoint neighborhoods of
be disjoint neighborhoods of  and
and  such that for every pair of distinct elements
such that for every pair of distinct elements
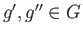 ,
,
Then
Since  is a group of homeomorphisms, it follows from the definition of quotient topology
that
is a group of homeomorphisms, it follows from the definition of quotient topology
that 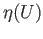 and
and 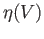 are open sets containing
are open sets containing 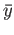 and
and 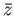 . It is easy to see that
. It is easy to see that
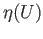 and
and 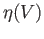 are disjoint and (i) follows and also that
are disjoint and (i) follows and also that 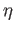 is an open mapping. Now
is an open mapping. Now
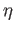 restricted to each
restricted to each 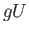 is a continuous, open bijection, that is a homeomorphism onto
is a continuous, open bijection, that is a homeomorphism onto 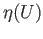 and so (ii)
follows.
Conclusion (iv) follows from (iii). To prove (iii) first observe that the map
and so (ii)
follows.
Conclusion (iv) follows from (iii). To prove (iii) first observe that the map
is a deck transformation for each 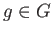 . The map
. The map
is easily seen to be a group homomorphism. To see that it is surjective,
let  be a deck transformation and
be a deck transformation and 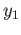 be a given point in
be a given point in  and
and
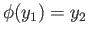 . Since
. Since 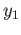 and
and 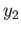 are in the same fiber,
there is a unique element
are in the same fiber,
there is a unique element 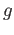 of the group such that
of the group such that
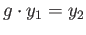 . Then the deck
transformations
. Then the deck
transformations  and
and 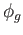 agree at
agree at 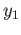 and so are identical which means
and so are identical which means
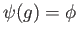 proving surjectivity. If
proving surjectivity. If 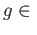 ker
ker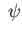 then
then
Since the action is properly discontinuous (and hence fixed point free) this forces 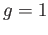 .
nisha
2012-03-20
.
nisha
2012-03-20