We shall show that if
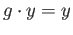 for some
for some 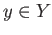 and
and 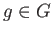 then
then 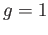 . If
. If 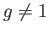 , choose a neighborhood
, choose a neighborhood  of
of 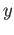 as in definition (20.1) which in particular
implies
as in definition (20.1) which in particular
implies
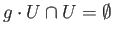 . But
. But
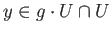 and we get a contradiction.
and we get a contradiction.
The set of all orbits of the action with its quotient topology is denoted by 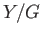 and the following theorem
expresses the covering properties of the quotient map
and the following theorem
expresses the covering properties of the quotient map
Note that for each 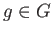 , the map
, the map
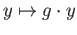 is a bijective map. If each of these maps is a
homeomorphism of
is a bijective map. If each of these maps is a
homeomorphism of  onto itself, we say that
onto itself, we say that  acts as a group of homeomorphisms on
acts as a group of homeomorphisms on  .
.
nisha
2012-03-20
![]() and the following theorem
expresses the covering properties of the quotient map
and the following theorem
expresses the covering properties of the quotient map