Let us assume that the following continuous time system is subject to sampling process with an interval of T.

We know that the solution to above state equation is:

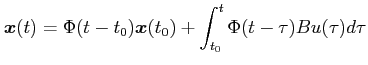
$\displaystyle \boldsymbol{x}(t) = \Phi (t-t_0) \boldsymbol{x}(t_0)+\int_{t_0}^t \Phi (t-\tau) Bu(\tau)d\tau$

Since the inputs are constants in between two sampling instants, one can write:

$\displaystyle u(\tau) = u(kT) \;\;\;\;$ for $\displaystyle , \;\; kT \le \tau \le (k+1)T$

which implies that the following expression is valid within the interval $kT \le \tau \le (k+1)T$ if we consider :

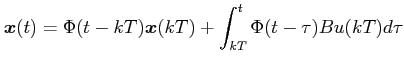
$\displaystyle \boldsymbol{x}(t) = \Phi (t-kT) \boldsymbol{x}(kT)+\int_{kT}^t \Phi (t-\tau) Bu(kT)d\tau$

Let us denote 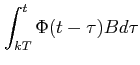$\displaystyle \int_{kT}^t \Phi (t-\tau) B d\tau$ by $\theta(t-KT)$ . Then we can write:

$\displaystyle \boldsymbol{x}(t) = \Phi (t-kT) \boldsymbol{x}(kT)+\theta(t-KT)u(kT)$

If ,

$\displaystyle \boldsymbol{x}((k+1)T) = \Phi (T) \boldsymbol{x}(kT)+\theta(T)u(kT)$

(4)