1.2.1 Effect of sampling period T
As can be seen from the previous example, large T has detrimental effect on relative stability. A thumb rule is to sample eight to ten times during a cycle of the damped sinusoidal oscillation of the output if it is underdamped. If overdamped, 8/10 times during rise time.
As seen from the example making the sampling period smaller allows the critical gain to be larger, i.e., maximum allowable gain can be made larger by increasing sampling frequency /rate.
It seems from the example that damping ratio decreases with the decrease in T. But one should take a note that damping ratio of the closed loop poles of a digital control system indicates the relative stability only if the sampling frequency is sufficiently high (8 to 10 times). If it is not the case, prediction of overshoot from the damping ratio will be erroneous and in practice the overshoot will be much higher than the predicted one.
Next, we may investigate the effect of T on the steady state error. Let us take a fixed gain K = 2.
When T = 0.5 sec. and K = 2,
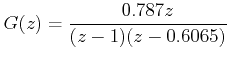 |
Since this is a second order system, velocity error constant will be a non zero finite quantity.
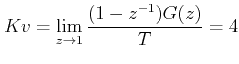
Thus, 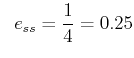
When T = 1 sec. and K = 2
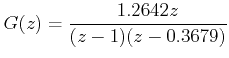 |
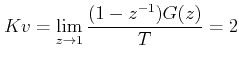
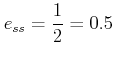
When T = 2 sec. and K = 2
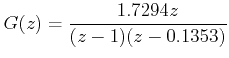 |
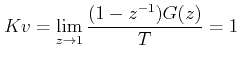
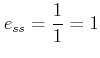
Thus, increasing sampling period (decreasing sampling frequency) has an adverse effect on the steady state error as well.