Module 5 : Design of Sampled Data Control Systems

Lecture 1 : Design based on root locus method

So far we have discussed about the modelling of a discrete time system by pulse transfer function, various stability tests and time domain performance criteria. The main objective of a control system is to design a controller either in forward or in feedback path so that the closed loop system is stable with some desired performance. Two most popular design techniques for continuous time LTI systems are using root locus and frequency domain methods.

1 Design based on root locus method

In many LTI discrete time control systems, the characteristics equation may have either of the following two forms.


$\displaystyle 1+G(z)H(z)$
 $\displaystyle =$ 0
$\displaystyle 1+GH(z)$
 $\displaystyle =$ 0


To combine both, let us define the characteristics equation as:

 

$\displaystyle 1+L(z)=0$
 (1)


where, $ L(z)=G(z)H(z)$ or $ L(z)=GH(z)$. $ L(z)$ is popularly known as the loop pulse transfer function. From equation (1), we can write

$\displaystyle L(z)=-1 $

Since $ L(z)$ is a complex quantity it can be split into two equations by equating angles and magnitudes of two sides. This gives us the angle and magnitude criteria as

Angle Criterion: $\displaystyle \;\;\;\;\;\;\angle L(z)= \pm 180^{0}(2k+1), \;\;\; k=0,1,2....$

Magnitude Criterion: $\displaystyle \;\;\;\;\;\; \vert L(z)\vert=1 $

The values of z that satisfy both criteria are the roots of the characteristics equation or close loop poles. Before constructing the root locus, the characteristics equation $ 1+L(z)=0$ should be rearranged in the following form

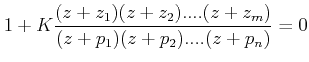$\displaystyle 1+K\frac{(z+z_{1})(z+z_{2})....(z+z_{m})}{(z+p_{1})(z+p_{2})....(z+p_{n})}=0$

where $ z_{i}$'s and $ p_{i}$'s are zeros and poles of open loop transfer function, m is the number of zeros n is the number of poles.