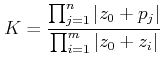1.1 Construction Rules for Root Locus

Root locus construction rules for digital systems are same as that of continuous time systems.

1. The root locus is symmetric about real axis. Number of root locus branches equals the number of open loop poles.

2. The root locus branches start from the open loop poles at K = 0 and ends at open loop zeros at K = ∞. In absence of open loop zeros, the locus tends to ∞ when K → ∞. Number of branches that tend to ∞ is equal to difference between the number of poles and number of zeros.

3. A portion of the real axis will be a part of the root locus if the number of poles plus number of zeros to the right of that portion is odd.

4. If there are n open loop poles and m open loop zeros then n - m root locus branches tend to ∞ along the straight line asymptotes drawn from a single point s = σ which is called centroid of the loci.

Angle of asymptotes 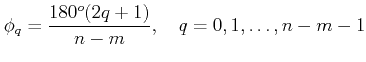$\displaystyle \phi_q=\frac{180^o(2q+1)}{n-m}, \quad q=0,1, \ldots, n-m-1$

5. Breakaway (Break in) points or the points of multiple roots are the solution of the following equation:

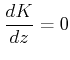
$\displaystyle \frac{dK}{dz} = 0$

where K is expressed as a function of z from the characteristic equation. This is a necessary but not sufficient condition. One has to check if the solutions lie on the root locus.

6. The intersection (if any) of the root locus with the imaginary axis can be determined from the Routh array.

7. The angle of departure from a complex open loop pole is given by

$\displaystyle \phi_p = 180^o + \phi$

where $\phi$ is the net angle contribution of all other open loop poles and zeros to that pole.

$\displaystyle \phi = \sum_i \psi_i - \sum_{j\neq p} \gamma_j$

$\psi_i$ 's are the angles contributed by zeros and $\gamma_j$ 's are the angles contributed by the poles.

8. The angle of arrival at a complex zero is given by

$\displaystyle \phi_z = 180^o - \phi$

where $\phi$ is same as in the above rule.

9. The gain at any point on the root locus is given by

$\displaystyle K=\frac{\prod_{j=1}^n \vert z_0+p_j\vert}{\prod_{i=1}^m \vert z_0+z_i\vert }$