Example 5: The characteristic equation: $P(z)= z^{3}+0.25z^{2}+z+0.25=0$

Thus, $a_{0}=1$ $a_{1}=0.25$ $a_{2}=1$ $a_{3}=0.25$ .

We will now check the stability conditions.

1. $\vert a_{n}\vert = \vert a_{3}\vert = 0.25 < a_{0}=1 \Rightarrow$ First condition is satisfied.

2. $P(1)=1+0.25+1+0.25=2.5>0 \Rightarrow$ Second condition is satisfied.

3. $P(-1)= -1+0.25-1+0.25=-1.5<0 \Rightarrow$ Third condition is satisfied.

Jury Table

Since the element b₁ is zero, we know that some of the roots lie on the unit circle.

If we replace z by (1 + ε) z, the characteristic equation would become:

$\displaystyle (1+3\epsilon) z^3 + 0.25(1+2\epsilon)z^2 + (1+\epsilon)z + 0.25 = 0$

First three stability conditions are satisfied when ε → 0⁺.

Jury Table

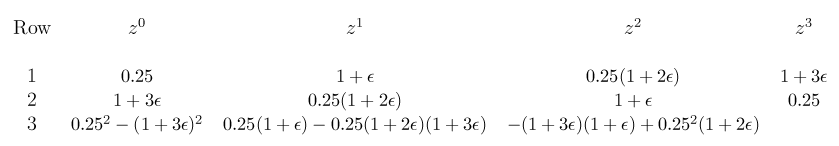
$\vert b_2\vert=\vert.0625-(1+6\epsilon+9\epsilon^2)\vert$ and $\vert b_0\vert=\vert 0.0625-(1+3.875\epsilon+3\epsilon^2)\vert$ .

Since, when ε → 0⁺, $1+6\epsilon+9\epsilon^2> 1+3.875\epsilon+3\epsilon^2$ , thus $\vert b_2\vert>\vert b_0\vert$ which implies that the roots which are not on the unit circle are actually inside it and the system is marginally stable. The roots of the characteristic equation are found out to be ±i and – 0.25 which verifies our conclusion.