1 Stability Analysis of closed loop system in z-plane

Stability is the most important issue in control system design. Before discussing the stability test let us first introduce the following notions of stability for a linear time invariant (LTI) system.

1. BIBO stability or zero state stbaility

2. Internal stability or zero input stability

Since we have not introduced the concept of state variables yet, as of now, we will limit our discussion to BIBO stability only.

An initially relaxed (all the initial conditions of the system are zero) LTI system is said to be BIBO stable if for every bounded input, the output is also bounded.

However, similar to continuous time systems, the stability of the following closed loop system

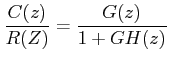
$\displaystyle \frac {C(z)}{R(Z)}= \frac {G(z)}{1+GH(z)}$
can also be determined from the location of closed loop poles in z-plane which are the roots of the characteristic equation

$\displaystyle 1+GH(z)=0$

1. For the system to be stable, the closed loop poles or the roots of the characteristic equation must lie within the unit circle in z-plane. Otherwise the system would be unstable.

2. If a simple pole lies at $\vert z\vert = 1$ , the system becomes marginally stable. Similarly if a pair of complex conjugate poles lie on the $\vert z\vert = 1$ circle, the system is marginally stable. Multiple poles at the same location on unit circle make the system unstable.

Example 1:

Determine the closed loop stability of the system shown in Figure 1 when K = 1.

**Figure 1:** Example 1
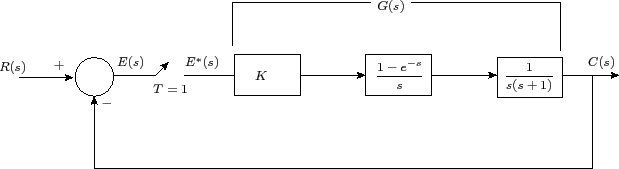$\begin{figure}\centering \input{m3l1f1.pstex_t}\end{figure}$

Solution:

$\displaystyle G(z)$		$\displaystyle =$ $\displaystyle Z\left[\frac {1-e^{-s}}{s}.\frac {1}{s(s+1)}\right]$
		$\displaystyle =$ $\displaystyle (1-z^{-1})Z\left[\frac{1}{s^{2}(s+1)}\right]$