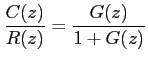
Since , and $\dfrac{C(z)}{R(z)}=\dfrac{G(z)}{1+G(z)}$
can be simplified as

$% latex2html id marker 657 $\displaystyle \therefore \frac {C(z)}{R(z)}$$		$\displaystyle =$ $\displaystyle \frac{z-1}{z}.\left[\frac{z}{(z-1)^{2}}-\frac{(1-e^{-1})z}{(z-1)(z-e^{-1})}\right]$
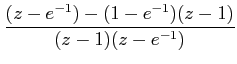		$\displaystyle =$ $\displaystyle \frac {(z-e^{-1})-(1-e^{-1})(z-1)}{(z-1)(z-e^{-1})}$
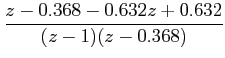		$\displaystyle =$ $\displaystyle \frac{z-0.368-0.632z+0.632}{(z-1)(z-0.368)}$
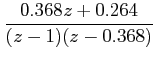		$\displaystyle =$ $\displaystyle \frac{0.368z+0.264}{(z-1)(z-0.368)}$

We know that the characteristics equation is $\Rightarrow 1+G(z)=0$

	$\displaystyle \Rightarrow$	$\displaystyle (z-1)(z-0.368)+ 0.368z+0.264=0$
	$\displaystyle \Rightarrow$	$\displaystyle z^{2}-z+0.632=0$
	$\displaystyle \Rightarrow$	$\displaystyle z_{1}=0.5+0.618j$
	$\displaystyle \Rightarrow$	$\displaystyle z_{2}=0.5-0.618j$

Since $\vert z_{1}\vert=\vert z_{2}\vert$ <1, the system is stable.

Three stability tests can be applied directly to the characteristic equation without solving for the roots.
→ Schur-Cohn stability test
→ Jury Stability test
→ Routh stability coupled with bi-linear transformation.

Other stability tests like Lyapunov stability analysis are applicable for state space system models which will be discussed later. Computation requirements in Jury test is simpler than Schur-Cohn when the co-efficients are real which is always true for physical systems.