Example 3: The characteristic equation is $P(z)=z^{3}-1.3z^{2}-0.08z+0.24=0$
Thus $a_{0}=1$ $a_{1}=-1.3$ $a_{2}=-0.08$ $a_{3}=0.24$ .

Stability conditions are:

1. $\vert a_{3}\vert=0.24 < a_{0}=1 \Rightarrow$ First condition is satisfied.

2. $P(1)=1-1.3-0.08+0.24 = -0.14 <0 \Rightarrow$ Second condition is not satisfied.

Since one of the criteria is violated, we may stop the test here and conclude that the system is unstable. or indicates the presence of a root on the unit circle and in that case the system can at the most become marginally stable if rest of the conditions are satisfied.

The stability range of a parameter can also be found from Jury's test which we will see in the next example.

Example 4: Consider the system shown in Figure 1. Find out the range of K for which the system is stable.

Solution:

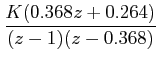$\displaystyle G(z)$		$\displaystyle =$ $\displaystyle \frac {K(0.368z+0.264)}{(z-1)(z-0.368)}$
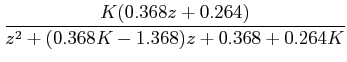The closed loop transfer function: $\displaystyle \frac {C(z)}{R(z)}$		$\displaystyle =$ $\displaystyle \frac {K(0.368z+0.264)}{z^{2}+(0.368K-1.368)z+0.368+0.264K}$

Characteristic equation: $P(z)=z^{2}+(0.368K-1.368)z+0.368+0.264K=0$
Since it is a second order system only 3 stability conditions will be there.