Combining all, the range of K is found to be 0 < K < 2.39 .

If K = 2.39 , system becomes critically stable. The characteristics equation becomes:

$z^{2}-0.49z+1=0$ $\Rightarrow z=0.244\pm j0.97$

Sampling period T = 1 sec.

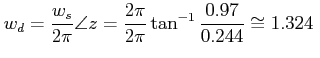$\displaystyle w_{d}=\dfrac{w_{s}}{2\pi} \angle z = \frac {2\pi}{2\pi} \tan^{-1}\frac {0.97}{0.244} \cong 1.324 \;$ rad/sec $\displaystyle$

The above frequency is the frequency of sustained oscillation.

1.2 Singular Cases

The situation, when some or all of the elements of a row in the Jury table are zero, indicates the presence of roots on the unit circle. This is referred to as a singular case.

It can be avoided by expanding or contracting unit circle infinitesimally by an amount ε which is equivalent to move the roots of P(z) off the unit circle. The transformation is:

$\displaystyle z_1=(1+\epsilon)z$
where ε is a very small number. When ε is positive the unit circle is expanded and when ε is negative the unit circle is contracted. The difference between the number of zeros found inside or outside the unit circle when the unit circle is expanded or contracted is the number of zeros on the unit circle.

Since $(1+\epsilon)^n z^n \cong (1+n\epsilon) z^n$ for both positive and negative ε, the transformation requires the coefficient of the zⁿ term be multiplied by $(1+n\epsilon)$ .