1.1 Characteristics Equation

Characteristics equation plays an important role in the study of linear systems. As said earlier, an n^th order LTI discrete data system can be represented by an n^th order difference equation,

$\displaystyle c(k+n)+a_{n-1}c(k+n-1)+a_{n-2}c(k+n-2)+...+a_{1}c(k+1)+a_0 c(k)$

$\displaystyle = b_m r(k+m) + b_{m-1} r(k+m-1) +...+ b_{0}r(k)$

where r(k) and c(k) denote input and output sequences respectively

The input output relation can be obtained by taking Z-transformation on both sides, with zero initial conditions, as

$\displaystyle G(z)$	$\displaystyle =$	$\displaystyle \frac{C(z)}{R(z)}$
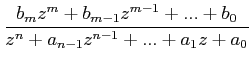	$\displaystyle =$	$\displaystyle \frac{b_{m}z^{m}+b_{m-1}z^{m-1}+...+b_{0}}{z^{n}+a_{n-1}z^{n-1}+...+a_{1}z+a_{0}}$	(6)

The characteristics equation is obtained by equating the denominator of G(z) to 0, as

$\displaystyle z^{n}+a_{n-1}z^{n-1}+...+a_{1}z+a_{0}=0$

Example
Consider the forward path transfer function as 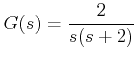$G(s)=\dfrac{1}{s(s+2)}$ and the feedback transfer function as 1. If the sampler is placed in the forward path, find out the characteristics equation of the overall system for a sampling period T = 0.1 sec.