Solution of two dimensional diffusion equation

The one-dimensional diffusion equation can be written as

                                                                         (40.20)

Consider the following initial and boundary conditions

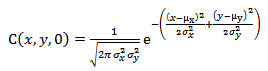                                              (40.21)

                                                                                      (40.22)

                                                                                       (40.23)

                                                                                     (40.24)

                                                                                     (40.25)

In this case also, we will transform the equation (40.20) using the following dimensionless variables to have better numerical stability.

                                                                                              (40.26)

                                                                                            (40.27)

                                                                                                 (40.28)

Where L₁ and L₂ are the length and width of the aquifer and is the simulation time .

Now we can have

                                                                               (40.29)

Similarly, we have

                                                                                        (40.30)

And,

                                                                                         (40.31)

Putting equation (40.29), (40.30), and (40.31) in (40.20), we have

                                                              (40.32)

                                                                (40.33)

Considering, D_x = D_y = D and for square domain (L₁ = L₂ = L ) and also considering

                                                                                                    (40.34)

We have

                                                                                 (40.35)

Now the initial and boundary conditions will be

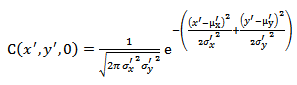                                      (40.36)

                                                                                       (40.37)

                                                                                       (40.38)

                                                                                      (40.39)

                                                                                       (40.40)

n+1

n