In this lecture, we will solve the diffusion and advection diffusion equations using finite difference method. Initially, we will solve the one-dimensional diffusion and advection-diffusion equations and then the methodology for solving the two-dimensional diffusion equation will also be discussed .

Solution of one dimensional diffusion equation

The one-dimensional diffusion equation can be written as

Solution of one dimensional diffusion equation

The one-dimensional diffusion equation can be written as

                                                                                                   (40.1)

Consider the following initial and boundary conditions

                                                                              (40.2)

                                                                                                   (40.3)

                                                                                                    (40.4)

The initial condition considered here is a Gaussian distribution. Other initial condition can also be used. The finite difference method can be applied directly to solve the equation (40.1) along with the initial and boundary conditions specified in equations (40.2), (40.3), and (40.4). However, we will transform the equation initially using the following dimensionless variables to have better numerical stability.

                                                                                                        (40.5)

                                                                                                          (40.6)

Where L is the length of the aquifer and is the simulation time .

                                                               (40.7)

Similarly, we have

                                                              (40.8)

                                                                                                  (40.9)

Putting equation (40.7) and (40.9) in (40.1), we have

                                                                                             (40.10)

                                                                                               (40.11)

Considering

                                                                                                             (40.12)

We have

                                                                                                     (40.13)

Now the initial and boundary conditions will be

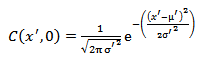                                                                        (40.14)

                                                                                                     (40.15)

                                                                                                    (40.16)

• 
• Fig. 40.1 Discretized 1D domain