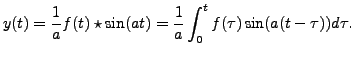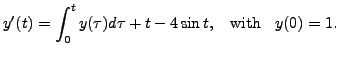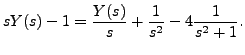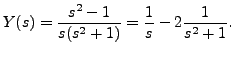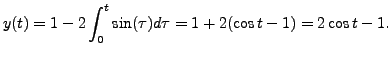Consider the following example.
EXAMPLE 10.5.1
Solve the following Initial Value Problem:
Solution: Let
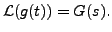 Then
Then
and the initial conditions imply
Hence,
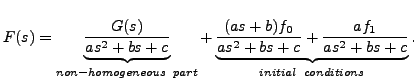 |
(10.5.1) |
Now, if we know that 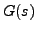 is a rational function of
is a rational function of 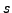 then we can
compute
then we can
compute 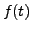 from
from 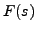 by using the method of
PARTIAL FRACTIONS (see Subsection 10.3.1).
by using the method of
PARTIAL FRACTIONS (see Subsection 10.3.1).
EXAMPLE 10.5.2
- Solve the IVP
with
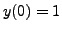 and
and
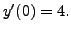
Solution: Note that
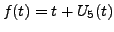 . Thus,
. Thus,
Taking Laplace transform of the above equation, we get
Which gives
Hence,
Remark 10.5.3
Even though 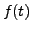 is a DISCONTINUOUS function at
is a DISCONTINUOUS function at 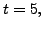 the solution
the solution 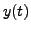 and
and
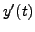 are continuous functions of
are continuous functions of 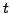 ,
as
,
as
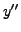 exists.
In general, the following is always true:
exists.
In general, the following is always true:
Let 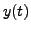 be a solution
of
be a solution
of
 Then both
Then both 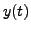 and
and
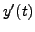 are continuous functions of time.
are continuous functions of time.
EXAMPLE 10.5.4
-
Consider the IVP
 with
with 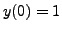 and
and
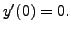 Find
Find
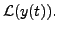
Solution: Applying Laplace transform, we have
Using initial conditions, the above equation reduces to
This equation after simplification can be rewritten as
Therefore,
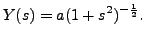 From Example
10.4.2.1, we see that
From Example
10.4.2.1, we see that 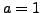 and hence
and hence
- Show that
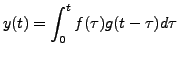 is a solution of
is a solution of
where
![$ {\mathcal
L}[g(t)] = \displaystyle\frac{1}{s^2 + a s + b}.$](img4820.png)
Solution: Here,
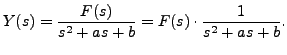 Hence,
Hence,
- Show that
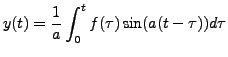 is a solution of
is a solution of
Solution: Here,
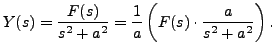 Hence,
Hence,
- Solve the following IVP.
Solution: Taking Laplace transform of both sides
and using Theorem 10.3.5, we get
Solving
for 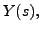 we get
we get
So,
A K Lal
2007-09-12
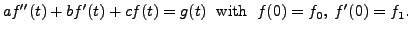
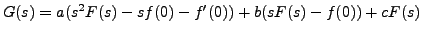
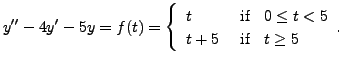
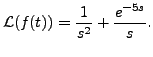
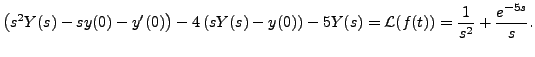
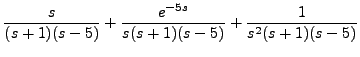
![$\displaystyle \frac{1}{6} \left[ \frac{5}{s-5} + \frac{1}{s+1} \right] + \frac{e^{-5s}}{30} \left[ -\frac{6}{s} +
\frac{5}{s+1} + \frac{1}{s-5} \right]$](img4800.png)
![$\displaystyle + \frac{1}{150} \left[ -\frac{30}{s^2} + \frac{24}{s} -
\frac{25}{s+1} + \frac{1}{s-5} \right].$](img4801.png)
![$\displaystyle \frac{5 e^{5t}}{6} +
\frac{e^{-t}}{6} + U_5(t)
\left[ -\frac{1}{5} + \frac{e^{-(t-5)}}{6} + \frac{e^{5(t-5)}}{30} \right]$](img4803.png)
![$\displaystyle + \frac{1}{150}
\left[ - 30 t + 24 - 25 e^{-t} + e^{5t} \right].$](img4804.png)
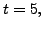 the solution
the solution ![$\displaystyle - \frac{d}{ds}\left[ s^2 Y(s) - s y(0) - y^\prime (0) \right] +
(s Y(s) - y(0)) - \frac{d}{ds} Y(s) = 0.$](img4812.png)
![$\displaystyle \frac{d}{ds} \left[ (s^2 +1) Y(s) - s \right] - s Y(s) + 1 = 0.$](img4813.png)
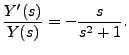
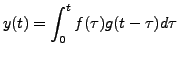 is a solution of
is a solution of
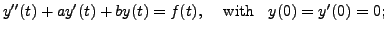
![$ {\mathcal
L}[g(t)] = \displaystyle\frac{1}{s^2 + a s + b}.$](img4820.png)
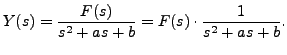 Hence,
Hence,
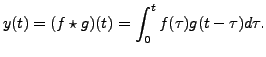
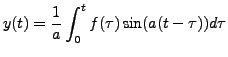 is a solution of
is a solution of
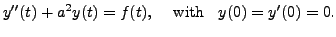
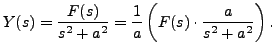 Hence,
Hence,