Next: Numerical Applications Up: Laplace Transform Previous: Application to Differential Equations Contents
Consider the following example.
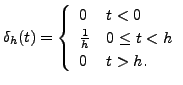
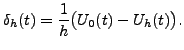 By linearity of the Laplace transform, we
get
By linearity of the Laplace transform, we
get
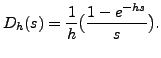
This new function is zero everywhere except at the origin. At origin, this function tends to infinity. In other words, the graph of the function appears as a line of infinite height at the origin. This new function,
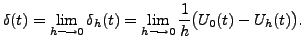
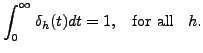
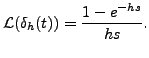 Now, if we take the
limit of both sides, as
Now, if we take the
limit of both sides, as
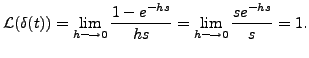
A K Lal 2007-09-12