Next: Inverse Transforms of Rational Up: Laplace Transform Previous: Examples Contents
The above lemma is immediate from the definition of Laplace transform and the linearity of the definite integral.
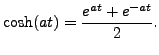 Thus
Thus
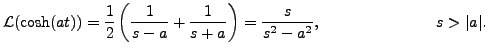
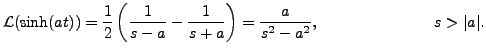
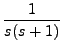 .
.
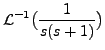 |
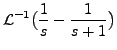 |
||
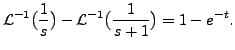 |
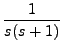 is
is
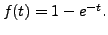
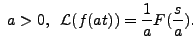
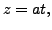 we get
we get
 |
|||
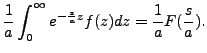 |
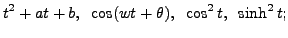
where
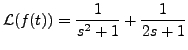 , find
, find
The next theorem relates the Laplace transform of the function
![]() with that of
with that of ![]() .
.
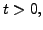 be a differentiable function
with the derivative,
be a differentiable function
with the derivative,
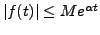 for all
for all
So, by definition,
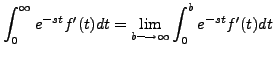 |
|||
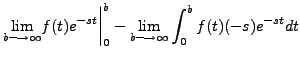 |
|||
We can extend the above result for
![]() derivative of
a function
derivative of
a function ![]() , if
, if
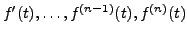 exist and
exist and
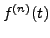 is continuous for
is continuous for ![]() . In this case, a repeated
use of Theorem 10.3.5, gives the following corollary.
. In this case, a repeated
use of Theorem 10.3.5, gives the following corollary.
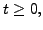 then
then
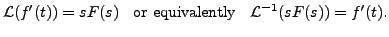
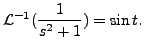 Then
Then
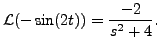
Now, using Theorem 10.3.5, we get
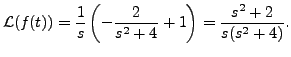
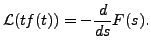
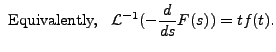
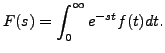 The result is
obtained by differentiating both sides with respect to
The result is
obtained by differentiating both sides with respect to
Suppose we know the Laplace transform of a ![]() and
we wish to find the Laplace transform of the function
and
we wish to find the Laplace transform of the function
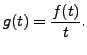 Suppose that
Suppose that
![]() exists. Then writing
exists. Then writing
![]() gives
gives
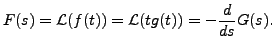
Thus,
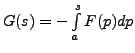 for some real number
for some real number 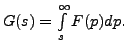
Hence,we have the following corollary.
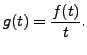 Then
Then
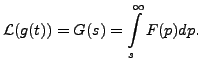
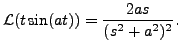
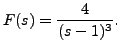
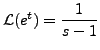 and
and
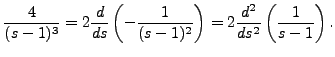
By lemma 10.3.9, we know that
![]() Suppose
Suppose
![]() Then
Then
![]() Therefore,
Therefore,
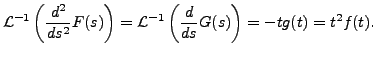
Thus we get
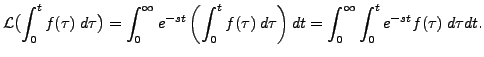
We don't go into the details of the proof of the change in the order of integration. We assume that the order of the integrations can be changed and therefore
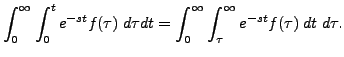
Thus,
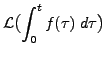 |
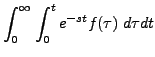 |
||
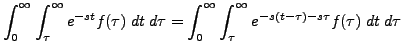 |
|||
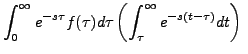 |
|||
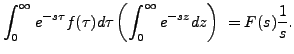 |
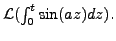
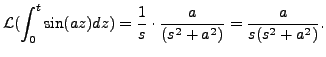
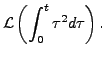
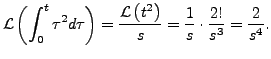
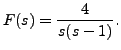
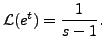 So,
So,
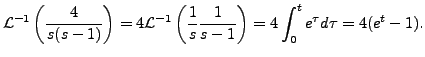
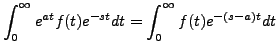 |
|||
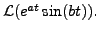
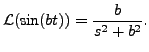 Hence
Hence
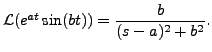
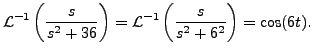
Hence,