Next: Properties of Laplace Transform Up: Definitions and Examples Previous: Definitions and Examples Contents
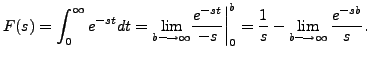
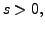 then
then
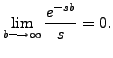
Thus,
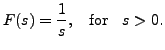
In the remaining part of this chapter, whenever the improper integral is calculated, we will not explicitly write the limiting process. However, the students are advised to provide the details.
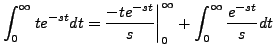 |
|||
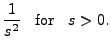 |
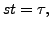 we get
we get
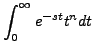 |
|||
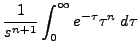 |
|||
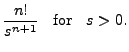 |
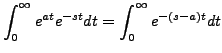 |
|||
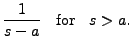 |
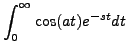 |
|||
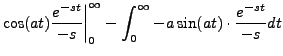 |
|||
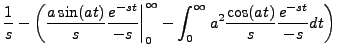 |
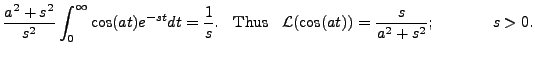
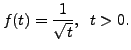
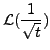 |
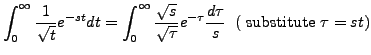 |
||
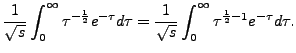 |
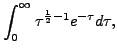 one needs to consider the double integral
one needs to consider the double integral
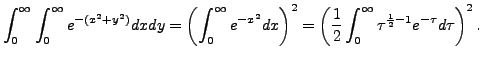
It turns out that
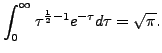
Thus,
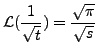 for
for
We now put the above discussed examples in tabular form as they
constantly appear in applications of
Laplace transform to differential equations.
A K Lal 2007-09-12