DEFINITION 10.2.1 (Piece-wise Continuous Function)
- A function
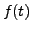 is said to be a piece-wise continuous function
on a closed interval
is said to be a piece-wise continuous function
on a closed interval
![$ [a, b] \subset {\mathbb{R}}$](img4536.png) , if there exists finite number of
points
, if there exists finite number of
points
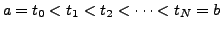 such that
such that
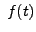 is continuous
in each of the intervals
is continuous
in each of the intervals
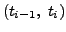 for
for
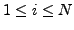 and has finite limits as
and has finite limits as 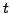 approaches the end points, see the Figure 10.1.
approaches the end points, see the Figure 10.1.
- A function
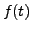 is said to be a piece-wise continuous function
for
is said to be a piece-wise continuous function
for 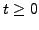 , if
, if 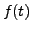 is a piece-wise continuous function
on every closed interval
is a piece-wise continuous function
on every closed interval
![$ [a, b] \subset [0, \infty).$](img4542.png) For example, see
Figure 10.1.
For example, see
Figure 10.1.
Figure 10.1:
Piecewise Continuous Function
|
|
Remark 10.2.3
- Let
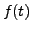 be an EXPONENTIALLY
BOUNDED function, i.e.,
be an EXPONENTIALLY
BOUNDED function, i.e.,
Then the Laplace transform of 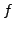 exists.
exists.
- Suppose
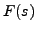 exists for some function
exists for some function 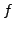 . Then by definition,
. Then by definition,
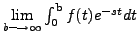 exists. Now, one can use the theory of improper integrals to conclude that
exists. Now, one can use the theory of improper integrals to conclude that
Hence, a function 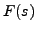 satisfying
satisfying
cannot be a Laplace transform of a function 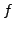 .
.
DEFINITION 10.2.4 (Inverse Laplace Transform)
Let
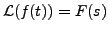 . That is,
. That is, 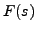 is the Laplace
transform of the function
is the Laplace
transform of the function 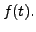 Then
Then 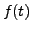 is called the
inverse Laplace transform of
is called the
inverse Laplace transform of 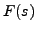 . In that case, we write
. In that case, we write
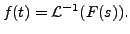
Subsections
A K Lal
2007-09-12
 , if
, if 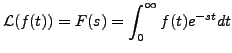
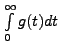 exists if
exists if
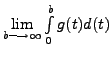 exists and we define
exists and we define
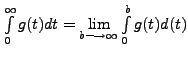 .)
.)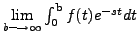 exists. Now, one can use the theory of improper integrals to conclude that
exists. Now, one can use the theory of improper integrals to conclude that