Next: Transform of Unit Step Up: Properties of Laplace Transform Previous: Properties of Laplace Transform Contents
Let ![]() be a rational function of
be a rational function of ![]() . We give a few examples to
explain the methods for calculating the inverse Laplace transform
of
. We give a few examples to
explain the methods for calculating the inverse Laplace transform
of ![]()
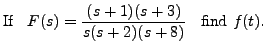
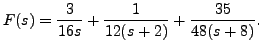 Thus,
Thus,
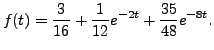
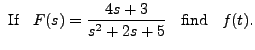
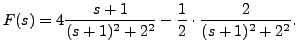 Thus,
Thus,
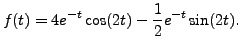
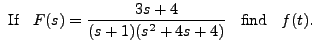
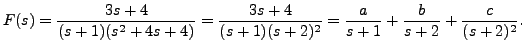
Solving for