Next: Application to Differential Equations Up: Some Useful Results Previous: Some Useful Results Contents
The following two theorems give us the behaviour of the function
![]() when
when
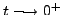 and when
and when
![]() .
.
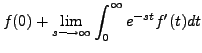 |
|||
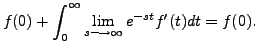 |
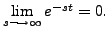 height6pt width 6pt depth 0pt
height6pt width 6pt depth 0pt
On similar lines, one has the following theorem. But this theorem
is valid only when ![]() is bounded as
is bounded as ![]() approaches infinity.
approaches infinity.
provided that
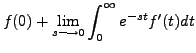 |
|||
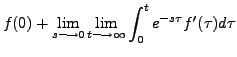 |
|||
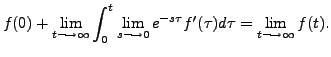 |
We now generalise the lemma on Laplace transform of an integral as convolution theorem.
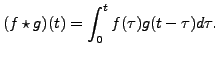
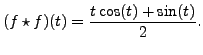
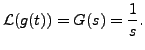 Thus, the Convolution Theorem
10.4.6 reduces to the Integral Lemma 10.3.12.
Thus, the Convolution Theorem
10.4.6 reduces to the Integral Lemma 10.3.12.A K Lal 2007-09-12