Next: Method of Reduction of Up: More on Second Order Previous: More on Second Order Contents
In this subsection, we discuss the linear independence or dependence of two solutions of Equation (8.2.1).
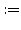 |
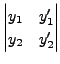 |
||
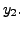
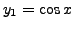 and
and
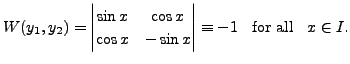 |
(8.2.2) |
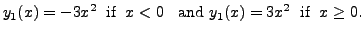
Therefore, for
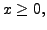
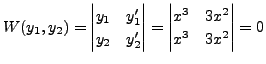
and for
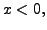
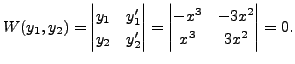
That is, for all
It is also easy to note that 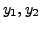 are linearly independent
on
are linearly independent
on ![]() In fact,they are
linearly independent on any interval
In fact,they are
linearly independent on any interval ![]() containing
containing ![]()
Given two solutions ![]() and
and ![]() of Equation (8.2.1),
we have a characterisation for
of Equation (8.2.1),
we have a characterisation for ![]() and
and ![]() to be linearly independent.
to be linearly independent.
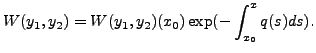 |
(8.2.3) |
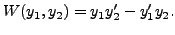
So
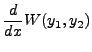 |
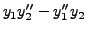 |
(8.2.4) | |
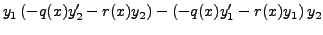 |
(8.2.5) | ||
| (8.2.6) | |||
| (8.2.7) |
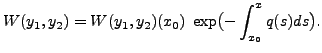
This completes the proof of the first part.
The second part follows the moment we note that the exponential function does
not vanish. Alternatively,
![]() satisfies a first order linear
homogeneous equation and therefore
satisfies a first order linear
homogeneous equation and therefore
height6pt width 6pt depth 0pt
Suppose not. Then
![]() So, by Theorem 2.5.1
the equations
So, by Theorem 2.5.1
the equations
Let
![]() Note that
Equation (8.2.8) now implies
Note that
Equation (8.2.8) now implies
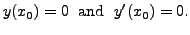
Therefore, by Picard's Theorem on existence and uniqueness of solutions (see Theorem 8.1.9), the solution
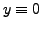 on
on
Suppose that
![]() for some
for some
![]() Therefore, by Theorem 8.2.4,
Therefore, by Theorem 8.2.4,
![]() for
all
for
all ![]() Suppose that
Suppose that
![]() for all
for all ![]() . Therefore,
. Therefore,
![]() for all
for all ![]() . Since
. Since
![]() in particular, we consider the linear system of equations
in particular, we consider the linear system of equations
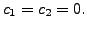 So,
by Definition 8.1.8,
So,
by Definition 8.1.8,
The following corollary is a consequence of Theorem 8.2.6.
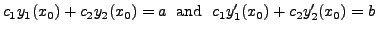 |
(8.2.10) |
A K Lal 2007-09-12