Next: Second Order equations with Up: More on Second Order Previous: Wronskian Contents
We are going to show that in order to find a fundamental system for Equation (8.2.1),
it is sufficient to have the knowledge of a solution of
Equation (8.2.1). In other words, if we know one (non-zero)
solution ![]() of Equation (8.2.1), then we can determine
a solution
of Equation (8.2.1), then we can determine
a solution ![]() of Equation (8.2.1), so that
of Equation (8.2.1), so that
![]() forms a fundamental system for Equation (8.2.1). The method is
described below and is usually called the method of reduction of order.
forms a fundamental system for Equation (8.2.1). The method is
described below and is usually called the method of reduction of order.
Let ![]() be an every where non-zero solution of Equation (8.2.1).
Assume that
be an every where non-zero solution of Equation (8.2.1).
Assume that
![]() is a solution of
Equation (8.2.1), where
is a solution of
Equation (8.2.1), where ![]() is to be determined. Substituting
is to be determined. Substituting
![]() in Equation (8.2.1), we have (after a bit of
simplification)
in Equation (8.2.1), we have (after a bit of
simplification)
By letting
which is same as
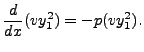
This is a linear equation of order one (hence the name, reduction of order) in
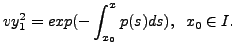
Substituting
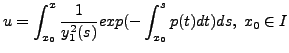
and hence a second solution of Equation (8.2.1) is
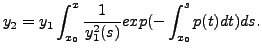
It is left as an exercise to show that ![]() are linearly independent. That is,
are linearly independent. That is,
![]() form a fundamental system for Equation (8.2.1).
form a fundamental system for Equation (8.2.1).
We illustrate the method by an example.
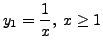 is a
solution of
is a
solution of
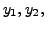 for
for 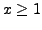 are linearly independent.
are linearly independent.
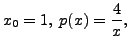 and
and
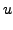 |
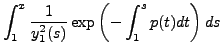 |
||
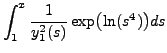 |
|||
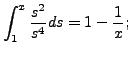 |
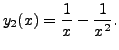
Since the term
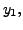 we can take
we can take
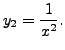 So,
So,
A K Lal 2007-09-12