Next: Wronskian Up: Second Order and Higher Previous: Introduction Contents
In this section, we wish to study some more properties of second order equations which have nice applications. They also have natural generalisations to higher order equations.
The general solution ![]() of Equation
(8.2.1) is defined by
of Equation
(8.2.1) is defined by
where
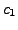 and
and 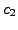 are arbitrary real
constants. Note that
are arbitrary real
constants. Note that
In other words, the general solution of Equation
(8.2.1) is a ![]() -parameter family of
solutions, the parameters being
-parameter family of
solutions, the parameters being ![]() and
and