Next: More on Second Order Up: Second Order and Higher Previous: Second Order and Higher Contents
Second order and higher order equations occur frequently in science and engineering (like pendulum problem etc.) and hence has its own importance. It has its own flavour also. We devote this section for an elementary introduction.
Here ![]() is an interval
contained in
is an interval
contained in
![]() and the functions
and the functions
![]() and
and
![]() are real valued
continuous functions defined on
are real valued
continuous functions defined on
![]() The functions
The functions
![]() and
and ![]() are called the coefficients of
Equation (8.1.1)
and
are called the coefficients of
Equation (8.1.1)
and ![]() is called the non-homogeneous term or the force function.
is called the non-homogeneous term or the force function.
Equation (8.1.1) is called linear homogeneous
if
![]() and non-homogeneous if
and non-homogeneous if
![]()
Recall that a second order equation is called nonlinear if it is not linear.
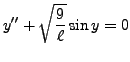
is a second order equation which is nonlinear.
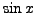 and
and We now state an important theorem whose proof is simple and is omitted.
 the function
the function
 is also a solution of Equation
(8.1.2).
is also a solution of Equation
(8.1.2). It is to be noted here that Theorem 8.1.5 is not an existence theorem. That is, it does not assert the existence of a solution of Equation (8.1.2).
For example, all the solutions of the Equation (8.1.2) form a
solution space. Note that
![]() is also a solution of
Equation (8.1.2). Therefore, the solution set of a
Equation (8.1.2) is non-empty. A moments reflection on Theorem
8.1.5 tells us that the solution space of Equation (8.1.2)
forms a real vector space.
is also a solution of
Equation (8.1.2). Therefore, the solution set of a
Equation (8.1.2) is non-empty. A moments reflection on Theorem
8.1.5 tells us that the solution space of Equation (8.1.2)
forms a real vector space.
The natural question is to inquire about its dimension. This question will be answered in a sequence of results stated below.
We first recall the definition of Linear Dependence and Independence.
The functions
To proceed further and to simplify matters, we assume that
![]() in Equation (8.1.2) and that the
function
in Equation (8.1.2) and that the
function ![]() and
and ![]() are continuous on
are continuous on ![]()
In other words, we consider a homogeneous linear equation
The next theorem, given without proof, deals with the existence and
uniqueness of solutions
of Equation (8.1.3) with initial conditions
![]() for some
for some
![]()
A word of Caution: NOTE THAT THE COEFFICIENT OF
An important application of Theorem 8.1.9 is that
the equation (8.1.3) has exactly
Use initial condition on
We now show that any solution of Equation (8.1.3) is a linear
combination of
![[*]](crossref.png) ) IS
) IS
![[*]](crossref.png) , WE HAVE TO ENSURE THIS
CONDITION.
, WE HAVE TO ENSURE THIS
CONDITION.
![]() linearly
independent solutions. In other words, the set of all solutions
over
linearly
independent solutions. In other words, the set of all solutions
over
![]() forms a real vector space of dimension
forms a real vector space of dimension ![]()
![]() and
and ![]() be real valued continuous functions on
be real valued continuous functions on ![]() Then
Equation (8.1.3) has exactly two linearly
independent solutions. Moreover, if
Then
Equation (8.1.3) has exactly two linearly
independent solutions. Moreover, if ![]() and
and ![]() are two linearly
independent solutions of Equation (8.1.3), then the solution
space is a linear combination of
are two linearly
independent solutions of Equation (8.1.3), then the solution
space is a linear combination of ![]() and
and ![]() .
.![]() and
and ![]() be two unique solutions of Equation
(8.1.3) with initial conditions
be two unique solutions of Equation
(8.1.3) with initial conditions
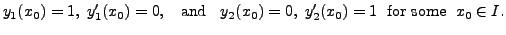
(8.1.5)
The unique solutions ![]() and
and ![]() exist by virtue of Theorem
8.1.9. We now claim that
exist by virtue of Theorem
8.1.9. We now claim that ![]() and
and ![]() are linearly
independent. Consider the system of linear equations
are linearly
independent. Consider the system of linear equations
where ![]() and
and ![]() are unknowns. If we can show that the only
solution for the system (8.1.6) is
are unknowns. If we can show that the only
solution for the system (8.1.6) is
![]() ,
then the two solutions
,
then the two solutions ![]() and
and ![]() will be linearly independent.
will be linearly independent.
![]() and
and ![]() to show that the only solution is indeed
to show that the only solution is indeed
![]() . Hence the result follows.
. Hence the result follows.
![]() and
and ![]() .
Let
.
Let ![]() be any solution of Equation
(8.1.3) and let
be any solution of Equation
(8.1.3) and let
![]() and
and
![]() Consider the function
Consider the function ![]() defined by
defined by
![]()
![]() is a solution of
Equation (8.1.3). Also note that
is a solution of
Equation (8.1.3). Also note that
![]() and
and
![]() So,
So, ![]() and
and ![]() are two
solution of Equation (8.1.3) with the same
initial conditions. Hence by Picard's Theorem on Existence and
Uniqueness (see Theorem 8.1.9),
are two
solution of Equation (8.1.3) with the same
initial conditions. Hence by Picard's Theorem on Existence and
Uniqueness (see Theorem 8.1.9),
![]() or
or
![]()
![]()
![]() and
and ![]() corresponding to the
initial conditions
corresponding to the
initial conditions 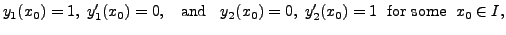
Consider a
![]() non-singular matrix
non-singular matrix
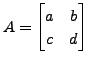 with
with
![]() Let
Let
![]() be a fundamental
system for the differential Equation 8.1.3 and
be a fundamental
system for the differential Equation 8.1.3 and
![$ {\mathbf y}^t = [y_1, \; y_2 ].$](img3778.png) Then the rows of the matrix
Then the rows of the matrix
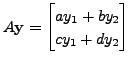 also form a fundamental system for
Equation 8.1.3. That is, if
also form a fundamental system for
Equation 8.1.3. That is, if
![]() is a fundamental
system for Equation 8.1.3 then
is a fundamental
system for Equation 8.1.3 then
![]() is also a fundamental system whenever
is also a fundamental system whenever
![]()
![]() is a fundamental system for
is a fundamental system for
![]()
Note that
![]() is also a fundamental
system. Here the matrix is
is also a fundamental
system. Here the matrix is
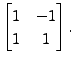
![]()
![]()
![]()
![]()
![]() and
and
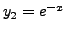 are solutions of
are solutions of
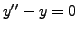
![]() and
and ![]() are
also solutions of
are
also solutions of
![]() Do
Do ![]() and
and ![]() form a fundamental set of solutions?
form a fundamental set of solutions?![]() forms a basis for the solution space of
forms a basis for the solution space of
![]() find another basis.
find another basis.