Next: Non Homogeneous Equations Up: Second Order and Higher Previous: Method of Reduction of Contents
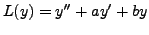
and
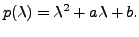
It is easy to note that
Now, it is clear that
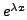 is a solution of Equation (8.3.1)
if and only if
is a solution of Equation (8.3.1)
if and only if
Case 1: Let
![]() be real roots of
Equation (8.3.2) with
be real roots of
Equation (8.3.2) with
![]()
Then
![]() and
and
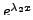 are two solutions of
Equation (8.3.1) and moreover they are linearly independent
(since
are two solutions of
Equation (8.3.1) and moreover they are linearly independent
(since
![]() ). That is,
). That is,
![]() forms a
fundamental system of solutions of Equation (8.3.1).
forms a
fundamental system of solutions of Equation (8.3.1).
Case 2: Let
![]() be a repeated root of
be a repeated root of
![]()
Then
![]() Now,
Now,
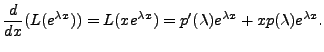
But
Hence,
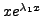 are two linearly independent solutions of
Equation (8.3.1). In this case,
we have a fundamental system of solutions of Equation (8.3.1).
are two linearly independent solutions of
Equation (8.3.1). In this case,
we have a fundamental system of solutions of Equation (8.3.1).
Case 3: Let
![]() be a complex root of
Equation (8.3.2).
be a complex root of
Equation (8.3.2).
So,
![]() is also a root of Equation (8.3.2).
Before we proceed, we note:
is also a root of Equation (8.3.2).
Before we proceed, we note:
Let
![]() be a complex root of
be a complex root of
![]() Then
Then
is a complex solution of Equation (8.3.1). By Lemma 8.3.2,
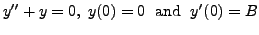
has a unique solution for any real number
A K Lal 2007-09-12