Next: Variation of Parameters Up: Second Order and Higher Previous: Second Order equations with Contents
Throughout this section, ![]() denotes an interval in
denotes an interval in
![]() we assume that
we assume that
![]() and
and ![]() are real valued continuous function
defined on
are real valued continuous function
defined on ![]() Now, we focus the attention to the study of non-homogeneous
equation of the form
Now, we focus the attention to the study of non-homogeneous
equation of the form
We assume that the functions
![]() and
and ![]() are
known/given. The non-zero function
are
known/given. The non-zero function ![]() in (8.4.1) is
also called the non-homogeneous term or the forcing function. The
equation
in (8.4.1) is
also called the non-homogeneous term or the forcing function. The
equation
Consider the set of all twice differentiable functions defined on ![]() We define an operator
We define an operator ![]() on this set by
on this set by
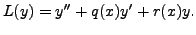
Then (8.4.1) and (8.4.2) can be rewritten in the (compact) form
| (8.4.3) | |||
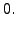 |
(8.4.4) |
The ensuing result relates the solutions of (8.4.1) and (8.4.2).
The linearity of
For the proof of second part, note that
implies that
Thus,
The above result leads us to the following definition.
where
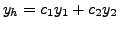 is a general solution of the
corresponding homogeneous equation (8.4.2) and
is a general solution of the
corresponding homogeneous equation (8.4.2) and 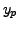 is
any solution of (8.4.1) (preferably containing no arbitrary
constants).
is
any solution of (8.4.1) (preferably containing no arbitrary
constants).We now prove that the solution of (8.4.1) with initial conditions is unique.
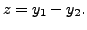 Then
Then
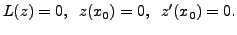
By the uniqueness theorem 8.1.9, we have
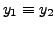 on
on
Then add the two solutions.
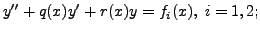
where
A K Lal 2007-09-12