Recall that
given a 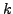 -dimensional vector subspace of a vector space
-dimensional vector subspace of a vector space  of dimension
of dimension
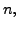 one can always find an
one can always find an 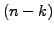 -dimensional vector subspace
-dimensional vector subspace 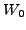 of
of  (see Exercise 3.3.20.9) satisfying
(see Exercise 3.3.20.9) satisfying
The subspace 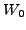 is called the complementary subspace of
is called the complementary subspace of 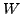 in
in 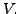 We now define an important class of linear transformations
on an inner product space, called orthogonal projections.
We now define an important class of linear transformations
on an inner product space, called orthogonal projections.
Remark 5.3.2
The map 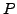 is well defined due to the following reasons:
is well defined due to the following reasons:
-
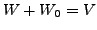 implies that for every
implies that for every
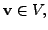 we can find
we can find
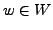 and
and
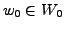 such that
such that
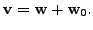
-
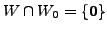 implies that the expression
implies that the expression
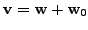 is unique for every
is unique for every
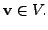
The next proposition states that the map defined above is a linear
transformation from  to
to 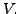 We omit the proof, as it follows directly
from the above remarks.
We omit the proof, as it follows directly
from the above remarks.
Remark 5.3.5
- The projection map
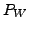 depends on the complementary subspace
depends on the complementary subspace 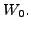
- Observe that for a fixed subspace
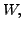 there are infinitely many choices
for the complementary subspace
there are infinitely many choices
for the complementary subspace 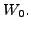
- It will be shown later that if
 is an inner product space with inner product,
is an inner product space with inner product,
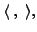 then the subspace
then the subspace 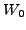 is unique if we put an additional condition that
is unique if we put an additional condition that
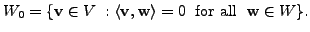
We now prove some basic properties about projection maps.
THEOREM 5.3.6
Let 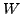 and
and 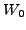 be complementary subspaces of a vector space
be complementary subspaces of a vector space 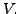 Let
Let
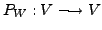 be a projection operator of
be a projection operator of  onto
onto 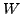 along
along 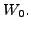 Then
Then
- the null space of
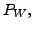
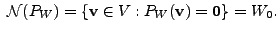
- the range space of
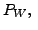
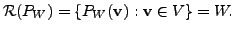
-
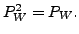 The condition
The condition
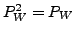 is equivalent to
is equivalent to
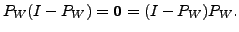
The next result uses the Gram-Schmidt orthogonalisation process to get
the complementary subspace in such a way that the vectors in different subspaces
are orthogonal.
DEFINITION 5.3.8 (Orthogonal Subspace of a Set)
Let  be an inner product space. Let
be an inner product space. Let 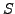 be a non-empty subset of
be a non-empty subset of  .
We define
.
We define
EXAMPLE 5.3.9
Let
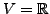 .
.
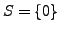 . Then
. Then
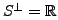 .
.
-
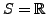 , Then
, Then
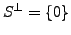 .
.
- Let
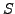 be any subset of
be any subset of
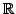 containing a non-zero real number. Then
containing a non-zero real number. Then
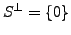 .
.
THEOREM 5.3.10
Let 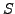 be a subset of a finite dimensional inner product space
be a subset of a finite dimensional inner product space 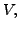 with inner product
with inner product
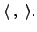 Then
Then
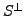 is a subspace of
is a subspace of 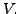
- Let
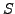 be equal to a subspace
be equal to a subspace 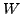 . Then the subspaces
. Then the subspaces 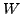 and
and 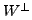 are complementary. Moreover, if
are complementary. Moreover, if
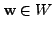 and
and
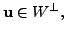 then
then
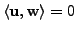 and
and
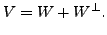
Proof.
We leave the prove of the first part for the reader. The prove of the
second part is as follows:
Let
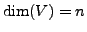
and
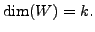
Let
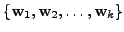
be a basis of
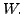
By Gram-Schmidt orthogonalisation process, we get an
orthonormal basis, say,
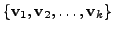
of
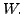
Then,
for any
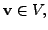
So,
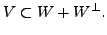
Also, for any
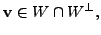
by definition of
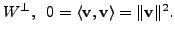
So,
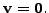
That is,
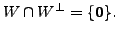
height6pt width 6pt depth 0pt
DEFINITION 5.3.12 (Self-Adjoint Transformation/Operator)
Let  be an inner product space with inner product
be an inner product space with inner product
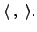 A linear transformation
A linear transformation
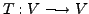 is called
a self-adjoint operator if
is called
a self-adjoint operator if
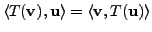 for every
for every
Remark 5.3.14
- By Proposition 5.3.3, the map
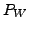 defined above
is a linear transformation.
defined above
is a linear transformation.
-
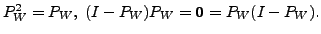
- Let
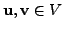 with
with
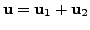 and
and
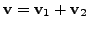 for some
for some
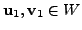 and
and
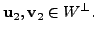 Then we know that
Then we know that
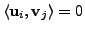 whenever
whenever
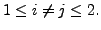 Therefore,
for every
Therefore,
for every
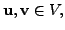
Thus, the orthogonal projection operator is a self-adjoint operator.
- Let
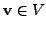 and
and
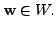 Then
Then
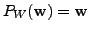 for all
for all
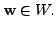 Therefore, using Remarks 5.3.14.2
and 5.3.14.3, we get
Therefore, using Remarks 5.3.14.2
and 5.3.14.3, we get
for every
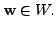
- In particular,
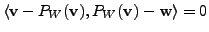 as
as
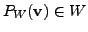 . Thus,
. Thus,
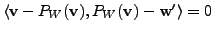 , for every
, for every
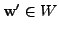 .
Hence, for any
.
Hence, for any
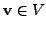 and
and
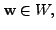 we have
we have
Therefore,
and the equality holds
if and only if
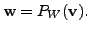 Since
Since
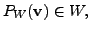 we see that
we see that
That is,
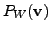 is the vector nearest to
is the vector nearest to
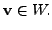 This can also be stated
as: the vector
This can also be stated
as: the vector
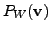 solves the following minimisation problem:
solves the following minimisation problem:
Subsections
A K Lal
2007-09-12
![]() -dimensional vector subspace of a vector space
-dimensional vector subspace of a vector space ![]() of dimension
of dimension
![]() one can always find an
one can always find an ![]() -dimensional vector subspace
-dimensional vector subspace ![]() of
of ![]() (see Exercise 3.3.20.9) satisfying
(see Exercise 3.3.20.9) satisfying
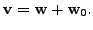
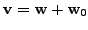 is unique for every
is unique for every
![]() to
to ![]() We omit the proof, as it follows directly
from the above remarks.
We omit the proof, as it follows directly
from the above remarks.
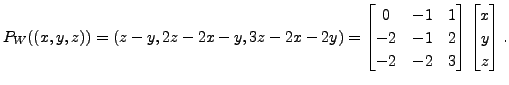
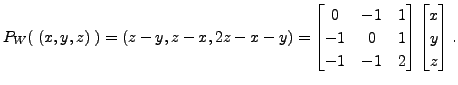
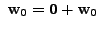 for
for
![]() let
let
![]() with
with
![]() for some
for some
![]() and
and
![]() Then by definition
Then by definition
![]() That is,
That is,
![]() and
and
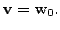 Thus,
Thus,
![]() Hence
Hence
![]() height6pt width 6pt depth 0pt
height6pt width 6pt depth 0pt
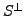 is a subspace of
is a subspace of 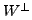 are complementary. Moreover, if
are complementary. Moreover, if
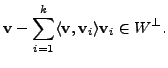
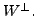
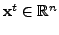 is a self-adjoint operator.
is a self-adjoint operator.
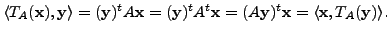
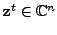 is a self-adjoint operator.
is a self-adjoint operator.