Next: Eigenvalues, Eigenvectors and Diagonalisation Up: Orthogonal Projections and Applications Previous: Orthogonal Projections and Applications Contents
The minimization problem stated above arises in lot of applications. So, it will be very helpful if the matrix of the orthogonal projection can be obtained under a given basis.
To this end, let ![]() be a
be a ![]() -dimensional subspace of
-dimensional subspace of
![]() with
with
![]() as its orthogonal
complement. Let
as its orthogonal
complement. Let
![]() be the orthogonal
projection of
be the orthogonal
projection of
![]() onto
onto ![]() .
Suppose, we are given an orthonormal basis
.
Suppose, we are given an orthonormal basis
![]() of
of ![]() Under the assumption that
Under the assumption that ![]() is known, we explicitly give the
matrix of
is known, we explicitly give the
matrix of ![]() with respect to an extended ordered basis
of
with respect to an extended ordered basis
of
![]()
Let us extend the given ordered orthonormal basis ![]() of
of ![]() to get an orthonormal
ordered basis
to get an orthonormal
ordered basis
![]() of
of
![]() Then by Theorem 5.1.12, for any
Then by Theorem 5.1.12, for any
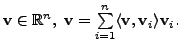 Thus, by definition,
Thus, by definition,
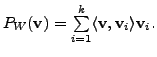 Let
Let
![]() Consider the
standard orthogonal ordered basis
Consider the
standard orthogonal ordered basis
![]() of
of
![]() Therefore, if
Therefore, if
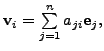 for
for
![]() then
then
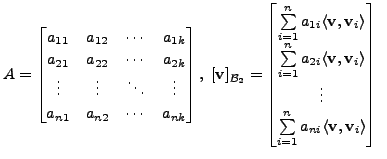
and
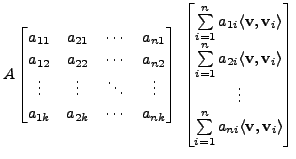
![$\displaystyle [P_W({\mathbf v})]_{{\cal B}_2} =
\begin{bmatrix}\sum\limits_{i=1...
...\limits_{i=1}^k a_{ni} \langle {\mathbf v}, {\mathbf v}_i\rangle
\end{bmatrix}.$](img2659.png)
Then as observed in Remark 5.2.3.4,
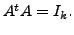 That is, for
That is, for
 |
|||
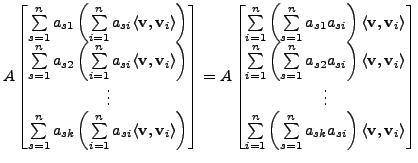 |
|||
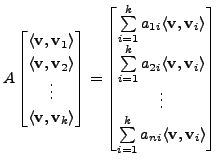 |
|||
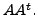
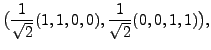
and that of
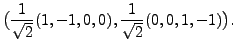
Therefore, if
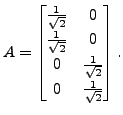
Hence, the matrix of the orthogonal projection
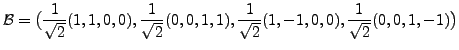
is
![$\displaystyle P_W[{\cal B},{\cal B}] = A A^t = \begin{bmatrix}\frac{1}{2} & \fr...
... \frac{1}{2} & \frac{1}{2} \\
0 & 0 & \frac{1}{2} & \frac{1}{2} \end{bmatrix}.$](img2677.png)
It is easy to see that
![$\displaystyle [(x,y,z,w)]_{{\cal B}} = \left(\frac{x+y}{\sqrt{2}}, \frac{z+w}{\sqrt{2}},
\frac{x-y}{\sqrt{2}},\frac{z-w}{\sqrt{2}}\right)^t.$](img2682.png)
Thus,
whenever