next up previous contents
Next: Gram-Schmidt Orthogonalisation Process Up: Inner Product Spaces Previous: Inner Product Spaces   Contents

Definition and Basic Properties

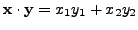In $ {\mathbb{R}}^2$ , given two vectors $ {\mathbf x}=(x_1, x_2), \; {\mathbf y}=(y_1, y_2)$ , we know the inner product $ {\mathbf x}\cdot {\mathbf y}= x_1 y_1 + x_2 y_2$ . Note that for any $ {\mathbf x}, {\mathbf y}, {\mathbf z}\in {\mathbb{R}}^2$ and $ {\alpha}\in {\mathbb{R}}$ , this inner product satisfies the conditions

$\displaystyle {\mathbf x}\cdot ({\mathbf y}+ {\alpha}{\mathbf z}) = {\mathbf x}... ...thbf y}\cdot {\mathbf x}, \; {\mbox{ and }} \; {\mathbf x}\cdot{\mathbf x}\ge 0$

and $ {\mathbf x}\cdot {\mathbf x}= 0$ if and only if $ {\mathbf x}={\mathbf 0}$ . Thus, we are motivated to define an inner product on an arbitrary vector space.

DEFINITION 5.1.1 (Inner Product)   Let $ V ({\mathbb{F}})$ be a vector space over $ {\mathbb{F}}.$ An inner product over $ V({\mathbb{F}}),$ denoted by $ \langle \;, \; \rangle,$ is a map,

$\displaystyle \langle \;, \; \rangle \; : V \times V \longrightarrow {\mathbb{F}}$

such that for $ {\mathbf u}, {\mathbf v}, {\mathbf w}\in V$ and $ a, b \in {\mathbb{F}}$
  1. $ \langle a {\mathbf u}+ b {\mathbf v}, {\mathbf w}\rangle = a \langle {\mathbf u}, {\mathbf w}\rangle + b \langle {\mathbf v}, {\mathbf w}\rangle,$
  2. $ \langle {\mathbf u}, {\mathbf v}\rangle = {\overline{\langle {\mathbf v}, {\mathbf u}\rangle}},$ the complex conjugate of $ \langle {\mathbf u}, {\mathbf v}\rangle, $ and
  3. $ \langle {\mathbf u}, {\mathbf u}\rangle \geq 0$ for all $ {\mathbf u}\in V$ and equality holds if and only if $ {\mathbf u}= {\mathbf 0}.$

DEFINITION 5.1.2 (Inner Product Space)   Let $ V$ be a vector space with an inner product $ \langle\; , \;\rangle.$ Then $ (V, \langle\; , \;\rangle)$ is called an inner product space, in short denoted by IPS.

EXAMPLE 5.1.3   The first two examples given below are called the STANDARD INNER PRODUCT or the DOT PRODUCT on $ {\mathbb{R}}^n$ and $ {\mathbb{C}}^n,$ respectively..
  1. Let $ V = {\mathbb{R}}^n $ be the real vector space of dimension $ n.$ Given two vectors $ {\mathbf u}= (u_1, u_2, \ldots, u_n)$ and $ {\mathbf v}=(v_1, v_2, \ldots, v_n)$ of $ V,$ we define

    $\displaystyle \langle u, v \rangle = u_1 v_1 + u_2 v_2 + \cdots + u_n v_n = {\mathbf u}{\mathbf v}^t.$

    Verify $ \langle \;, \; \rangle$ is an inner product.
  2. Let $ V= {\mathbb{C}}^n$ be a complex vector space of dimension $ n.$ Then for $ {\mathbf u}= (u_1, u_2, \ldots, u_n)$ and $ {\mathbf v}=(v_1, v_2, \ldots, v_n)$ in $ V,$ check that

    $\displaystyle \langle u, v \rangle = u_1 {\overline{v_1}} + u_2 {\overline{v_2}} + \cdots + u_n {\overline{v_n}} = {\mathbf u}{\mathbf v}^*$

    is an inner product.
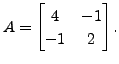  3. Let $ V = {\mathbb{R}}^2$ and let $ A = \begin{bmatrix}4 & -1 \\ -1 & 2 \end{bmatrix}.$ Define $ \langle {\mathbf x}, {\mathbf y}\rangle = {\mathbf x}A {\mathbf y}^{t}.$ Check that $ \langle \;, \; \rangle$ is an inner product. Hint: Note that $ {\mathbf x}A {\mathbf y}^{t} = 4 x_1 y_1 - x_1 y_2 - x_2 y_1 + 2 x_2 y_2.$
  4. let $ {\mathbf x}=(x_1,x_2,x_3), \; {\mathbf y}=(y_1,y_2,y_3) \in {\mathbb{R}}^3.,$ Show that $ \langle {\mathbf x},{\mathbf y}\rangle = 10 x_1 y_1 + 3 x_1 y_2 + 3 x_2 y_1 + 2 x_2 y_2 + x_2 y_3 + x_3 y_2 + x_3 y_3$ is an inner product in $ {\mathbb{R}}^3 ({\mathbb{R}}).$
  5. Consider the real vector space $ {\mathbb{R}}^2$ . In this example, we define three products that satisfy two conditions out of the three conditions for an inner product. Hence the three products are not inner products.
    1. Define $ \langle {\mathbf x}, {\mathbf y}\rangle = \langle (x_1, x_2), (y_1, y_2) \rangle = x_1 y_1.$ Then it is easy to verify that the third condition is not valid whereas the first two conditions are valid.
    2. Define $ \langle {\mathbf x}, {\mathbf y}\rangle = \langle (x_1, x_2), (y_1, y_2) \rangle = x_1^2 + y_1^2 + x_2^2 + y_2^2.$ Then it is easy to verify that the first condition is not valid whereas the second and third conditions are valid.
    3. Define $ \langle {\mathbf x}, {\mathbf y}\rangle = \langle (x_1, x_2), (y_1, y_2) \rangle = x_1y_1^3 + x_2 y_2^3.$ Then it is easy to verify that the second condition is not valid whereas the first and third conditions are valid.

Remark 5.1.4   Note that in parts $ 1$ and $ 2$ of Example 5.1.3, the inner products are $ {\mathbf u}{\mathbf v}^t$ and $ {\mathbf u}{\mathbf v}^{*}$ , respectively. This occurs because the vectors $ {\mathbf u}$ and $ {\mathbf v}$ are row vectors. In general, $ {\mathbf u}$ and $ {\mathbf v}$ are taken as column vectors and hence one uses the notation $ {\mathbf u}^t {\mathbf v}$ or $ {\mathbf u}^*{\mathbf v}$ .

EXERCISE 5.1.5   Verify that inner products defined in parts $ 3$ and $ 4$ of Example 5.1.3, are indeed inner products.

DEFINITION 5.1.6 (Length/Norm of a Vector)   For $ {\mathbf u}\in V,$ we define the length (norm) of $ {\mathbf u},$ denoted $ \Vert {\mathbf u}\Vert,$ by $ \Vert {\mathbf u}\Vert = \sqrt{\langle {\mathbf u}, {\mathbf u}\rangle},$ the positive square root.

A very useful and a fundamental inequality concerning the inner product is due to Cauchy and Schwartz. The next theorem gives the statement and a proof of this inequality.

THEOREM 5.1.7 (Cauchy-Schwartz inequality)   Let $ V ({\mathbb{F}})$ be an inner product space. Then for any $ {\mathbf u}, {\mathbf v}\in V$

$\displaystyle \vert \langle {\mathbf u}, {\mathbf v}\rangle \vert \leq \Vert {\mathbf u}\Vert \; \Vert {\mathbf v}\Vert.$

The equality holds if and only if the vectors $ {\mathbf u}$ and $ {\mathbf v}$ are linearly dependent. Further, if $ {\mathbf u}\neq {\mathbf 0}$ , then $ {\mathbf v}= \displaystyle \langle {\mathbf v}, \frac{{\mathbf u}}{\Vert {\mathbf u}\Vert} \rangle \frac{{\mathbf u}}{\Vert{\mathbf u}\Vert}.$

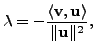Proof. If $ {\mathbf u}= {\mathbf 0},$ then the inequality holds. Let $ {\mathbf u}\neq {\mathbf 0}.$ Note that $ \langle {\lambda}{\mathbf u}+ {\mathbf v}, {\lambda}{\mathbf u}+ {\mathbf v}\rangle \geq 0$ for all $ {\lambda}\in {\mathbb{F}}.$ In particular, for $ {\lambda}= \displaystyle - \frac{\langle {\mathbf v},{\mathbf u}\rangle}{\Vert {\mathbf u}\Vert^2},$ we get
0 $\displaystyle \leq$ $\displaystyle \langle {\lambda}{\mathbf u}+ {\mathbf v}, {\lambda}{\mathbf u}+ {\mathbf v}\rangle$  
  $\displaystyle =$ $\displaystyle {\lambda}\overline{{\lambda}} \Vert{\mathbf u}\Vert^2 + {\lambda}... ...ne{{\lambda}} \langle {\mathbf v}, {\mathbf u}\rangle + \Vert{\mathbf v}\Vert^2$  
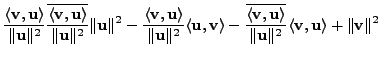  $\displaystyle =$ $\displaystyle \frac{\langle {\mathbf v},{\mathbf u}\rangle}{\Vert {\mathbf u}\V... ...bf u} \Vert^2}\langle {\mathbf v}, {\mathbf u}\rangle + \Vert{\mathbf v}\Vert^2$  
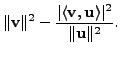  $\displaystyle =$ $\displaystyle \Vert{\mathbf v}\Vert^2 - \frac{\vert\langle {\mathbf v},{\mathbf u}\rangle\vert^2}{\Vert {\mathbf u}\Vert^2}.$  

Or, in other words

$\displaystyle \vert\langle {\mathbf v},{\mathbf u}\rangle\vert^2 \leq \Vert{\mathbf u}\Vert^2 \Vert{\mathbf v}\Vert^2$

and the proof of the inequality is over.

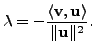Observe that if $ {\mathbf u}\neq {\mathbf 0}$ then the equality holds if and only of $ {\lambda}{\mathbf u}+ {\mathbf v}= {\mathbf 0}$ for $ {\lambda}= - \displaystyle \frac{\langle {\mathbf v}, {\mathbf u}\rangle }{\Vert {\mathbf u}\Vert^2}.$ That is, $ {\mathbf u}$ and $ {\mathbf v}$ are linearly dependent. We leave it for the reader to prove

$\displaystyle {\mathbf v}= \displaystyle \langle {\mathbf v}, \frac{{\mathbf u}}{\Vert {\mathbf u}\Vert} \rangle \frac{{\mathbf u}}{\Vert{\mathbf u}\Vert}.$

height6pt width 6pt depth 0pt

DEFINITION 5.1.8 (Angle between two vectors)   Let $ V$ be a real vector space. Then for every $ {\mathbf u}, {\mathbf v}\in V,$ by the Cauchy-Schwartz inequality, we have

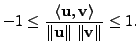
$\displaystyle -1 \leq \frac{\langle {\mathbf u}, {\mathbf v}\rangle}{\Vert{\mathbf u}\Vert \; \Vert{\mathbf v}\Vert} \leq 1.$

We know that 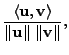$ \cos : [0, \pi] \longrightarrow [-1, \; 1]$ is an one-one and onto function. Therefore, for every real number $ \displaystyle\frac{\langle {\mathbf u}, {\mathbf v}\rangle}{\Vert{\mathbf u}\Vert \; \Vert{\mathbf v}\Vert},$ there exists a unique $ \theta, \; 0 \leq \theta \leq \pi,$ such that

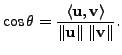
$\displaystyle \cos \theta = \frac{\langle {\mathbf u}, {\mathbf v}\rangle}{\Vert{\mathbf u}\Vert \; \Vert{\mathbf v}\Vert}.$

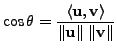  1. The real number $ \theta$ with $ 0 \leq \theta \leq \pi$ and satisfying $ \cos \theta = \displaystyle\frac{\langle {\mathbf u}, {\mathbf v}\rangle}{\Vert{\mathbf u}\Vert \; \Vert{\mathbf v}\Vert}$ is called the angle between the two vectors $ {\mathbf u}$ and $ {\mathbf v}$ in $ V.$
  2. The vectors $ {\mathbf u}$ and $ {\mathbf v}$ in $ V$ are said to be orthogonal if $ \langle {\mathbf u}, {\mathbf v}\rangle = 0.$
  3. A set of vectors $ \{{\mathbf u}_1, {\mathbf u}_2, \ldots, {\mathbf u}_n\} $ is called mutually orthogonal if $ \langle {\mathbf u}_i, {\mathbf u}_j \rangle = 0$ for all $ 1 \leq i \neq j \leq n.$

DEFINITION 5.1.9 (Orthogonal Complement)   Let $ W$ be a subspace of a vector space $ V$ with inner product $ \langle \;, \; \rangle$ . Then the subspace

$\displaystyle W^{\perp} = \{ {\mathbf v}\in V : \; \langle {\mathbf v}, {\mathbf w}\rangle = 0 \; {\mbox{ for all }} \;\; {\mathbf w}\in W\}$

is called the orthogonal complement of $ W$ in $ V.$

EXERCISE 5.1.10  
  1. Let $ \{{\mathbf e}_1, {\mathbf e}_2, \ldots, {\mathbf e}_n\}$ be the standard basis of $ {\mathbb{R}}^n.$ Then prove that with respect to the standard inner product on $ {\mathbb{R}}^n,$ the vectors $ {\mathbf e}_i$ satisfy the following:
    1. $ \Vert {\mathbf e}_i\Vert = 1$ for $ \; 1 \leq i \leq n.$
    2. $ \langle {\mathbf e}_i, {\mathbf e}_j \rangle = 0$ for $ 1 \leq i \neq j \leq n.$
  2. Recall the following inner product on $ {\mathbb{R}}^2: \; $ for $ {\mathbf x}= (x_1, x_2)^t$ and $ {\mathbf y}= (y_1, y_2)^t,$

    $\displaystyle \langle {\mathbf x}, {\mathbf y}\rangle = 4 x_1 y_1 - x_1 y_2 - x_2 y_1 + 2 x_2 y_2.$

    1. Find the angle between the vectors $ e_1 = (1,0)^t$ and $ e_2 = (0,1)^t.$
    2. Let $ {\mathbf u}= (1,0)^t.$ Find $ {\mathbf v}\in {\mathbb{R}}^2$ such that $ \langle {\mathbf v}, {\mathbf u} \rangle = 0.$
    3. Find two vectors $ {\mathbf x}, {\mathbf y}\in {\mathbb{R}}^2,$ such that $ \Vert{\mathbf x}\Vert = \Vert{\mathbf y}\Vert = 1$ and $ \langle {\mathbf x}, {\mathbf y}\rangle = 0.$
  3. Find an inner product in $ {\mathbb{R}}^2$ such that the following conditions hold:

    $\displaystyle \Vert (1, 2) \Vert = \Vert (2, -1) \Vert = 1, \;\; {\mbox{ and }} \;\; \langle (1, 2), \; (2, -1) \rangle = 0.$

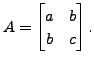    [Hint: Consider a symmetric matrix $ A = \begin{bmatrix}a & b \\ b & c \end{bmatrix}.$ Define $ \langle {\mathbf x}, {\mathbf y}\rangle = {\mathbf y}^t A {\mathbf x}$ and solve a system of $ 3$ equations for the unknowns $ a, b, c$ .]
  4. Let $ W = \{ (x,y,z) \in {\mathbb{R}}^3: x + y + z = 0 \}.$ Find $ W^{\perp}$ with respect to the standard inner product.
  5. Let $ W$ be a subspace of a finite dimensional inner product space $ V$ . Prove that $ (W^{\perp})^{\perp} = W.$
  6. Let $ V$ be a complex vector space with $ \dim (V) = n.$ Fix an ordered basis $ {\cal B}= ( {\mathbf u}_1, {\mathbf u}_2, \ldots, {\mathbf u}_n).$ Define a map

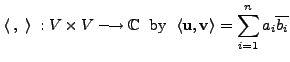
    $\displaystyle \langle\;, \; \rangle \; : V \times V \longrightarrow {\mathbb{C}... ...}} \; \langle {\mathbf u}, {\mathbf v}\rangle = \sum_{i=1}^n a_i \overline{b_i}$

    whenever $ [{\mathbf u}]_{{\cal B}} = (a_1, a_2, \ldots, a_n)^t$ and $ [{\mathbf v}]_{{\cal B}} = (b_1, b_2, \ldots, b_n)^t.$ Show that the above defined map is indeed an inner product.
  7. Let $ {\mathbf x}=(x_1,x_2,x_3), \; {\mathbf y}=(y_1,y_2,y_3) \in {\mathbb{R}}^3.$ Show that

    $\displaystyle \langle {\mathbf x},{\mathbf y}\rangle = 10 x_1 y_1 + 3 x_1 y_2 + 3 x_2 y_1 + 2 x_2 y_2 + x_2 y_3 + x_3 y_2 + x_3 y_3$

    is an inner product in $ {\mathbb{R}}^3 ({\mathbb{R}}).$ With respect to this inner product, find the angle between the vectors $ (1,1,1)$ and $ (2, -5, 2).$
  8. Consider the set $ M_{n \times n}({\mathbb{R}})$ of all real square matrices of order $ n.$ For $ A, B \in M_{n \times n}({\mathbb{R}})$ we define $ \langle A, B \rangle = tr(A B^{t}).$ Then

    $\displaystyle \langle A + B, C\rangle = tr\bigl( (A+B)C^t \bigr) = tr(A C^t) + tr(B C^t) = \langle A , C\rangle + \langle B, C\rangle.$

    $\displaystyle \langle A, B \rangle = tr(A B^t) = tr( \; (A B^t)^t\;) = tr(B A^t) = \langle B, A \rangle.$

    Let $ A = (a_{ij}).$ Then

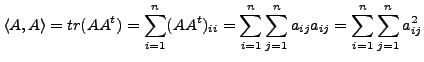
    $\displaystyle \langle A, A \rangle = tr(A A^t) = \sum_{i=1}^n (A A^t)_{ii} = \sum_{i=1}^n \sum_{j=1}^n a_{ij} a_{ij} = \sum_{i=1}^n \sum_{j=1}^n a_{ij}^2$

    and therefore, $ \langle A, A \rangle > 0$ for all non-zero matrices $ A.$ So, it is clear that $ \langle A, B \rangle$ is an inner product on $ M_{n \times n}({\mathbb{R}})$ .

    If $ W = \{ A \in M_{n \times n}({\mathbb{R}}) : \; A^t = A\}$ , determine $ W^{\perp}.$

  9. Let $ V$ be the real vector space of all continuous functions with domain $ [-2 \pi, 2 \pi].$ That is, $ V = C[-2 \pi, \; 2 \pi].$ Then show that $ V$ is an inner product space with inner product $ \int_{-1}^1 f(x) g(x) dx.$

    For different values of $ m$ and $ n,$ find the angle between the functions $ \cos (m x)$ and $ \sin (n x).$

  10. Let $ V$ be an inner product space. Prove that

    $\displaystyle \Vert {\mathbf u}+ {\mathbf v}\Vert \leq \Vert {\mathbf u}\Vert +... ... {\mathbf v}\Vert \;\; {\mbox{ for every }} \;\; {\mathbf u}, {\mathbf v}\in V.$

    This inequality is called the TRIANGLE INEQUALITY.
  11. Let $ z_1, z_2, \ldots, z_n \in {\mathbb{C}}.$ Use the Cauchy-Schwartz inequality to prove that

    $\displaystyle \vert z_1 + z_2 + \cdots + z_n\vert \leq \sqrt{n (\vert z_1\vert^2 + \vert z_2\vert^2 + \cdots + \vert z_n\vert^2)}.$

    When does the equality hold?
  12. Let $ {\mathbf x}, {\mathbf y}\in {\mathbb{R}}^n.$ Observe that $ \langle {\mathbf x}, {\mathbf y}\rangle = \langle {\mathbf y}, {\mathbf x}\rangle.$ Hence or otherwise prove the following:
    1. $ \langle {\mathbf x}, {\mathbf y}\rangle = 0 \Longleftrightarrow \Vert {\mathbf x}- {\mathbf y}\Vert^2 = \Vert{\mathbf x}\Vert^2 + \Vert{\mathbf y}\Vert^2, \;\;$ (This is called PYTHAGORAS THEOREM).
    2. $ \Vert {\mathbf x}\Vert= \Vert {\mathbf y}\Vert \Longleftrightarrow \langle {\mathbf x}+ {\mathbf y}, {\mathbf x}-{\mathbf y}\rangle = 0, \;\;$ ( $ {\mathbf x}$ and $ {\mathbf y}$ form adjacent sides of a rhombus as the diagonals $ {\mathbf x}+ {\mathbf y}$ and $ {\mathbf x}- {\mathbf y}$ are orthogonal).
    3. $ \Vert{\mathbf x}+ {\mathbf y}\Vert^2 + \Vert {\mathbf x}- {\mathbf y}\Vert^2 = 2 \Vert{\mathbf x}\Vert^2 + 2 \Vert{\mathbf y}\Vert^2, \;\;$ (This is called the PARALLELOGRAM LAW).
    4. $ 4 \langle {\mathbf x}, {\mathbf y}\rangle = \Vert {\mathbf x}+ {\mathbf y}\Vert^2 - \Vert {\mathbf x}- {\mathbf y}\Vert^2 $ (This is called the POLARISATION IDENTITY).

      Remark 5.1.11  
      1. Suppose the norm of a vector is given. Then, the polarisation identity can be used to define an inner product.
      2. Observe that if $ \langle {\mathbf x}, {\mathbf y}\rangle = 0$ then the parallelogram spanned by the vectors $ {\mathbf x}$ and $ {\mathbf y}$ is a rectangle. The above equality tells us that the lengths of the two diagonals are equal.



      Are these results true if $ {\mathbf x},{\mathbf y}\in {\mathbb{C}}^n ({\mathbb {C}})?$

  13. Let $ {\mathbf x}, {\mathbf y}\in {\mathbb{C}}^n ({\mathbb{C}}).$ Prove that
    1. $ 4 \langle {\mathbf x},{\mathbf y}\rangle = \Vert{\mathbf x}+ {\mathbf y}\Vert^... ...ert{\mathbf x}+ i{\mathbf y}\Vert^2 - i \Vert{\mathbf x}- i {\mathbf y}\Vert^2.$
    2. If $ {\mathbf x}\neq {\mathbf 0}$ then $ \;\; \Vert{\mathbf x}+ i {\mathbf x}\Vert^2 = \Vert{\mathbf x}\Vert^2 + \Vert i {\mathbf x}\Vert^2,$ even though $ \langle {\mathbf x}, i {\mathbf x}\rangle \neq 0.$
    3. If $ \Vert{\mathbf x}+ {\mathbf y}\Vert^2 = \Vert{\mathbf x}\Vert^2 + \Vert{\mathbf y}\Vert^2$ and $ \Vert{\mathbf x}+ i {\mathbf y}\Vert^2 = \Vert{\mathbf x}\Vert^2 + \Vert i {\mathbf y}\Vert^2$ then show that $ \langle {\mathbf x}, {\mathbf y}\rangle = 0.$
  14. Let $ \langle \;, \; \rangle$ denote the standard inner product on $ {\mathbb{C}}^n({\mathbb{C}})$ and let $ A$ be an $ n \times n$ matrix. Then prove that $ \langle {\mathbf x}, {\mathbf y}\rangle = {\mathbf x}{\mathbf y}^*$ and $ \langle {\mathbf x}A, {\mathbf y}\rangle = \langle {\mathbf x}, {\mathbf y}A^* \rangle$ for all $ {\mathbf x}, {\mathbf y}\in {\mathbb{C}}^n$ .

    Or equivalently, if $ {\mathbf u}$ and $ {\mathbf v}$ are column vectors then $ \langle A {\mathbf u}, {\mathbf v}\rangle = \langle {\mathbf u}, A^* {\mathbf v}\rangle$ .

  15. Let $ V$ be an $ n$ -dimensional inner product space, with an inner product $ \langle\; , \;\rangle.$ Let $ {\mathbf u}\in V$ be a fixed vector with $ \Vert {\mathbf u}\Vert = 1.$ Then give reasons for the following statements.
    1. Let $ S^{\perp} = \{ {\mathbf v}\in V \;: \; \langle {\mathbf v}, {\mathbf u}\rangle = 0 \}.$ Then $ S$ is a subspace of $ V$ of dimension $ n-1.$
    2. Let $ 0 \neq {\alpha}\in {\mathbb{F}}$ and let $ S = \{ {\mathbf v}\in V \;: \; \langle {\mathbf v}, {\mathbf u}\rangle={\alpha}\}.$ Then $ S$ is not a subspace of $ V.$
    3. For any $ {\mathbf v}\in S,$ there exists a vector $ {\mathbf v}_0 \in S^{\perp},$ such that $ {\mathbf v}= {\mathbf v}_0 + {\alpha}{\mathbf u}.$

THEOREM 5.1.12   Let $ V$ be an inner product space. Let $ \{{\mathbf u}_1, {\mathbf u}_2, \ldots, {\mathbf u}_n\} $ be a set of non-zero, mutually orthogonal vectors of $ V.$
  1. Then the set $ \{{\mathbf u}_1, {\mathbf u}_2, \ldots, {\mathbf u}_n\} $ is linearly independent.
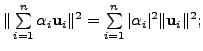
  2. $ \Vert \sum\limits_{i=1}^n \alpha_i {\mathbf u}_i \Vert^2 = \sum\limits_{i=1}^n \vert\alpha_i\vert^2 \Vert {\mathbf u}_i \Vert^2;$
  3. Let $ \dim(V) = n$ and also let $ \Vert{\mathbf u}_i\Vert = 1$ for $ i=1,2,\ldots,n.$ Then for any $ {\mathbf v}\in V,$

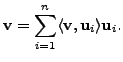
    $\displaystyle {\mathbf v}= \sum\limits_{i=1}^n \langle {\mathbf v}, {\mathbf u}_i \rangle {\mathbf u}_i.$

    In particular, $ \langle {\mathbf v}, {\mathbf u}_i \rangle = 0$ for all $ i = 1, 2, \ldots, n$ if and only if $ {\mathbf v}= {\mathbf 0}.$

Proof. Consider the set of non-zero, mutually orthogonal vectors $ \{{\mathbf u}_1, {\mathbf u}_2, \ldots, {\mathbf u}_n\}.$ Suppose there exist scalars $ c_1, c_2, \ldots, c_n$ not all zero, such that

$\displaystyle c_1 {\mathbf u}_1 + c_2 {\mathbf u}_2 + \cdots + c_n {\mathbf u}_n = {\mathbf 0}.$

Then for $ 1 \leq i \leq n,$ we have

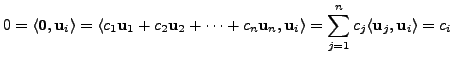
$\displaystyle 0 = \langle {\mathbf 0}, {\mathbf u}_i \rangle = \langle c_1 {\ma... ..._i \rangle = \sum_{j=1}^n c_j \langle {\mathbf u}_j, {\mathbf u}_i\rangle = c_i$

as $ \langle {\mathbf u}_j, {\mathbf u}_i\rangle = 0$ for all $ j \neq i$ and $ \langle {\mathbf u}_i, {\mathbf u}_i\rangle = 1.$ This gives a contradiction to our assumption that some of the $ c_i$ 's are non-zero. This establishes the linear independence of a set of non-zero, mutually orthogonal vectors.

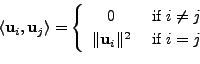For the second part, using \begin{displaymath}\langle {\mathbf u}_i, {\mathbf u}_j \rangle = \left\{ \begin... ... {\mathbf u}_i\Vert^2 & {\mbox{ if }} i = j \end{array} \right.\end{displaymath} for $ 1 \leq i, j \leq n,$ we have

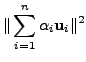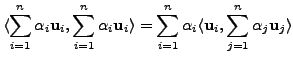$\displaystyle \Vert\sum_{i=1}^n {\alpha}_i {\mathbf u}_i \Vert^2$ $\displaystyle =$ $\displaystyle \langle \sum_{i=1}^n {\alpha}_i {\mathbf u}_i, \sum_{i=1}^n {\alp... ...{\alpha}_i \langle {\mathbf u}_i, \sum_{j=1}^n {\alpha}_j {\mathbf u}_j \rangle$  
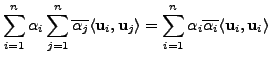  $\displaystyle =$ $\displaystyle \sum_{i=1}^n {\alpha}_i \sum_{j=1}^n \overline{{\alpha}_j} \langl... ...n {\alpha}_i \overline{{\alpha}_i} \langle {\mathbf u}_i, {\mathbf u}_i \rangle$  
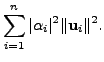  $\displaystyle =$ $\displaystyle \sum_{i=1}^n \vert{\alpha}_i\vert^2 \Vert {\mathbf u}_i\Vert^2.$  

For the third part, observe from the first part, the linear independence of the non-zero mutually orthogonal vectors $ {\mathbf u}_1, {\mathbf u}_2, \ldots, {\mathbf u}_n.$ Since $ \dim(V) = n,$ they form a basis of $ V.$ Thus, for every vector $ {\mathbf v}\in V,$ there exist scalars $ {\alpha}_i, \; 1 \leq i \leq n,$ such that $ {\mathbf v}= \sum_{i=1}^n {\alpha}_i {\mathbf u}_n.$ Hence,

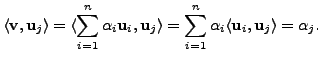
$\displaystyle \langle {\mathbf v}, {\mathbf u}_j \rangle = \langle \sum_{i=1}^n... ...m_{i=1}^n {\alpha}_i \langle {\mathbf u}_i, {\mathbf u}_j \rangle = {\alpha}_j.$

Therefore, we have obtained the required result. height6pt width 6pt depth 0pt

DEFINITION 5.1.13 (Orthonormal Set)   Let $ V$ be an inner product space. A set of non-zero, mutually orthogonal vectors $ \{{\mathbf v}_1, {\mathbf v}_2, \ldots, {\mathbf v}_n \}$ in $ V$ is called an orthonormal set if $ \Vert {\mathbf v}_i \Vert = 1$ for $ i=1,2,\ldots,n.$

If the set $ \{{\mathbf v}_1, {\mathbf v}_2, \ldots, {\mathbf v}_n \}$ is also a basis of $ V,$ then the set of vectors $ \{{\mathbf v}_1, {\mathbf v}_2, \ldots, {\mathbf v}_n \}$ is called an orthonormal basis of $ V.$

EXAMPLE 5.1.14  
  1. Consider the vector space $ {\mathbb{R}}^2$ with the standard inner product. Then the standard ordered basis $ {\cal B}= \bigl( (1,0), (0,1) \bigr)$ is an orthonormal set. Also, the basis $ {\cal B}_1 = \displaystyle \bigl( \frac{1}{\sqrt{2}}(1,1), \frac{1}{\sqrt{2}}(1,-1) \bigr)$ is an orthonormal set.
  2. Let $ {\mathbb{R}}^n$ be endowed with the standard inner product. Then by Exercise 5.1.10.1, the standard ordered basis $ ({\mathbf e}_1, {\mathbf e}_2, \ldots, {\mathbf e}_n)$ is an orthonormal set.

In view of Theorem 5.1.12, we inquire into the question of extracting an orthonormal basis from a given basis. In the next section, we describe a process (called the Gram-Schmidt Orthogonalisation process) that generates an orthonormal set from a given set containing finitely many vectors.

Remark 5.1.15   The last part of the above theorem can be rephrased as ``suppose $ \{{\mathbf v}_1, {\mathbf v}_2, \ldots, {\mathbf v}_n \}$ is an orthonormal basis of an inner product space $ V.$ Then for each $ {\mathbf u}\in V$ the numbers $ \langle {\mathbf u}, {\mathbf v}_i \rangle$ for $ 1 \leq i \leq n$ are the coordinates of $ {\mathbf u}$ with respect to the above basis".

That is, let $ {\cal B}= ({\mathbf v}_1, {\mathbf v}_2, \ldots, {\mathbf v}_n)$ be an ordered basis. Then for any $ {\mathbf u}\in V,$

$\displaystyle [{\mathbf u}]_{{\cal B}} = ( \langle {\mathbf u}, {\mathbf v}_1\r... ..., {\mathbf v}_2 \rangle, \ldots, \langle {\mathbf u}, {\mathbf v}_n \rangle)^t.$

next up previous contents
Next: Gram-Schmidt Orthogonalisation Process Up: Inner Product Spaces Previous: Inner Product Spaces   Contents
A K Lal 2007-09-12