DEFINITION 4.3.1 (Range and Null Space)
Let 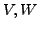 be finite dimensional vector spaces over the same set of
scalars and
be finite dimensional vector spaces over the same set of
scalars and
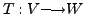 be a linear transformation. We define
be a linear transformation. We define
-
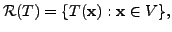 and
and
-
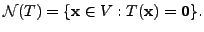
We now prove some results associated with the above definitions.
PROPOSITION 4.3.2
Let  and
and 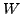 be finite dimensional vector spaces and let
be finite dimensional vector spaces and let
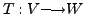 be a linear transformation. Suppose that
be a linear transformation. Suppose that
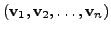 is an ordered basis of
is an ordered basis of 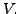 Then
Then
-
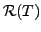 is a subspace of
is a subspace of 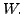
-
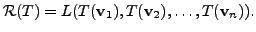
-
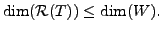
-
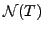 is a subspace of
is a subspace of 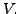
-
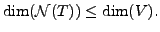
 is one-one
is one-one
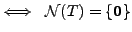 is the zero
subspace of
is the zero
subspace of
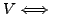
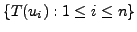 is a basis of
is a basis of
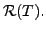
-
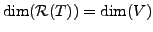 if and only if
if and only if
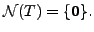
Proof.
The results about
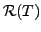
and
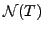
can be easily proved.
We thus leave the proof for the readers.
We now assume that

is one-one. We need to show
that
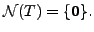
Let
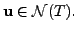
Then by definition,
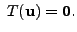
Also for
any linear transformation (see Proposition
4.1.3),
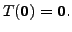
Thus
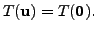
So,

is one-one implies
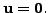
That is,
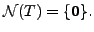
Let
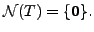 We need to show that
We need to show that  is one-one.
So, let us assume that for some
is one-one.
So, let us assume that for some
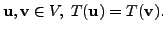 Then, by linearity of
Then, by linearity of
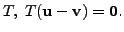 This implies,
This implies,
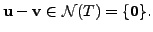 This in turn implies
This in turn implies
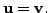 Hence,
Hence,  is one-one.
is one-one.
The other parts can be similarly proved.
height6pt width 6pt depth 0pt
Remark 4.3.3
- The space
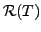 is called the RANGE SPACE of
is called the RANGE SPACE of  and
and
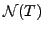 is called the NULL SPACE of
is called the NULL SPACE of 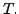
- We write
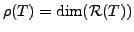 and
and
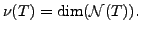
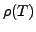 is called the rank of the linear transformation
is called the rank of the linear transformation  and
and 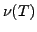 is called the nullity of
is called the nullity of 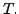
EXAMPLE 4.3.4
Determine the range and null space of the linear transformation
Solution: By Definition
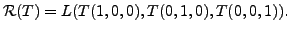 We therefore have
Also, by definition
We therefore have
Also, by definition
We now state and prove the rank-nullity Theorem. This result also
follows from Proposition 4.3.2.
THEOREM 4.3.6 (Rank Nullity Theorem)
Let
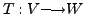 be a linear
transformation and
be a linear
transformation and  be a finite dimensional vector space. Then
be a finite dimensional vector space. Then
or equivalently
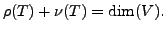
Proof.
Let
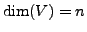
and
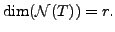
Suppose
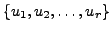
is a basis of
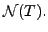
Since
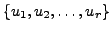
is a linearly independent set in
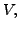
we can
extend it to form a basis of

(see Corollary
3.3.15).
So, there exist vectors
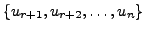
such that
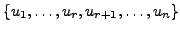
is a basis of
Therefore, by Proposition
4.3.2
We now prove that the set
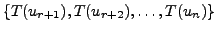
is linearly independent. Suppose the set is
not linearly independent. Then, there exists scalars,
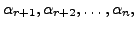
not all zero such that
That is,
So, by definition of
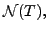
Hence, there exists scalars
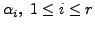
such that
That is,
But the set
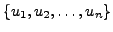
is a basis of

and so linearly independent.
Thus by definition of linear independence
In other words, we have shown that
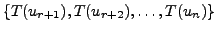
is a basis of
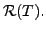
Hence,
height6pt width 6pt depth 0pt
Using the Rank-nullity theorem, we give a short proof of the following result.
COROLLARY 4.3.7
Let
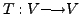 be a linear transformation on a finite dimensional
vector space
be a linear transformation on a finite dimensional
vector space 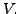 Then
Then
Proof.
By Proposition
4.3.2,

is one-one if and only if
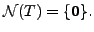
By the rank-nullity Theorem
4.3.6
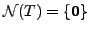
is equivalent to the condition
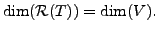
Or equivalently

is onto.
By definition,  is invertible if
is invertible if  is one-one and onto. But we have
shown that
is one-one and onto. But we have
shown that  is one-one if and only if
is one-one if and only if  is onto. Thus, we have
the last equivalent condition.
height6pt width 6pt depth 0pt
is onto. Thus, we have
the last equivalent condition.
height6pt width 6pt depth 0pt
Remark 4.3.8
Let  be a finite dimensional vector space and let
be a finite dimensional vector space and let
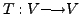 be a
linear transformation. If either
be a
linear transformation. If either  is one-one or
is one-one or  is onto, then
is onto, then
 is invertible.
is invertible.
The following are some of the consequences of
the rank-nullity theorem. The proof is left as an
exercise for the reader.
COROLLARY 4.3.9
The following are equivalent for an
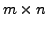 real matrix
real matrix 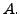
-
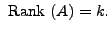
- There exist exactly
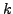 rows of
rows of  that are linearly independent.
that are linearly independent.
- There exist exactly
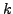 columns of
columns of  that are linearly independent.
that are linearly independent.
- There is a
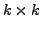 submatrix of
submatrix of  with non-zero determinant and
every
with non-zero determinant and
every
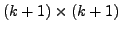 submatrix of
submatrix of  has zero determinant.
has zero determinant.
- The dimension of the range space of
 is
is 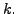
- There is a subset of
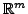 consisting of exactly
consisting of exactly 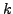 linearly independent vectors
linearly independent vectors
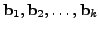 such that the system
such that the system
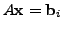 for
for
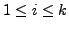 is consistent.
is consistent.
- The dimension of the null space of
A K Lal
2007-09-12
![]() We need to show that
We need to show that ![]() is one-one.
So, let us assume that for some
is one-one.
So, let us assume that for some
![]() Then, by linearity of
Then, by linearity of
![]() This implies,
This implies,
![]() This in turn implies
This in turn implies
![]() Hence,
Hence, ![]() is one-one.
is one-one.
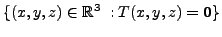
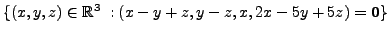
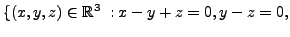
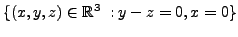
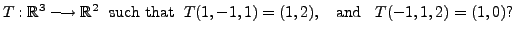
![]() is invertible if
is invertible if ![]() is one-one and onto. But we have
shown that
is one-one and onto. But we have
shown that ![]() is one-one if and only if
is one-one if and only if ![]() is onto. Thus, we have
the last equivalent condition.
height6pt width 6pt depth 0pt
is onto. Thus, we have
the last equivalent condition.
height6pt width 6pt depth 0pt
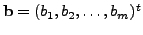 such that the system
such that the system
![$ [{\mathbf w}_i]_{{\cal B}} = [ a_{1i}, \;
a_{2i}, \ldots, a_{ni} \;]^t$](img1990.png) . Put
. Put
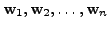 is a basis of
is a basis of 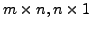 and
and
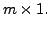 Define a linear transformation
Define a linear transformation
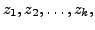 we define a linear transformation
we define a linear transformation