Next: Rank-Nullity Theorem Up: Linear Transformations Previous: Definitions and Basic Properties Contents
In this section, we relate linear transformation over finite dimensional vector spaces with matrices. For this, we ask the reader to recall the results on ordered basis, studied in Section 3.4.
Let ![]() and
and ![]() be finite dimensional vector spaces
over the set
be finite dimensional vector spaces
over the set
![]() with
respective dimensions
with
respective dimensions ![]() and
and ![]() Also, let
Also, let
![]() be a linear
transformation. Suppose
be a linear
transformation. Suppose
![]() is an
ORDERED BASIS of
is an
ORDERED BASIS of ![]() In the last section, we saw that
a linear transformation is determined by its image on a basis of the domain
space. We therefore look at the images of the vectors
In the last section, we saw that
a linear transformation is determined by its image on a basis of the domain
space. We therefore look at the images of the vectors
![]() for
for
![]()
Now for each
![]() the vectors
the vectors
![]() We
now express these
vectors in terms of an ordered basis
We
now express these
vectors in terms of an ordered basis
![]() of
of ![]() So, for each
So, for each
![]() there exist unique scalars
there exist unique scalars
![]() such that
such that
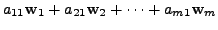 |
|||
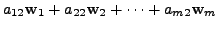 |
|||
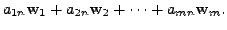 |
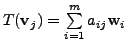 for
for
![$\displaystyle [T({\mathbf v}_j)]_{{\cal B}_2} = \begin{bmatrix}
a_{1j} \\ a_{2j} \\ \vdots \\ a_{mj} \end{bmatrix}.$](img1815.png)
Let
![$ [{\mathbf x}]_{{\cal B}_1} = [x_1, x_2, \ldots, x_n]^t$](img1816.png) be the
coordinates of a vector
be the
coordinates of a vector
![]() Then
Then
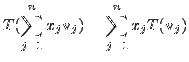 |
|||
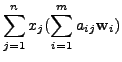 |
|||
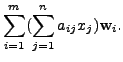 |
 Then the coordinates of the vector
Then the coordinates of the vector
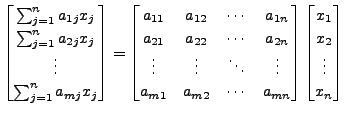 |
|||
We thus have the following theorem.
We now give a few examples to understand the above discussion and the theorem.
We obtain
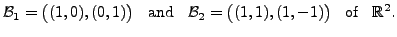
For any vector
![$\displaystyle (x,y) \in {\mathbb{R}}^2,
\; \; [(x,y)]_{{\cal B}_1} = \begin{bmatrix}x \\ y \end{bmatrix}$](img1837.png)
as
and
That is,
![$ \; [T(\;(0,1)\;)]_{{\cal B}_2} = (0,1)^t.$](img1842.png) So
the
So
the
![$ T[{\cal B}_1, {\cal B}_2] = \begin{bmatrix}1 & 0 \\ 0 & 1 \end{bmatrix}.$](img1843.png) Observe that in this case,
Observe that in this case,
![$\displaystyle [T(\;(x,y) \;)]_{{\cal B}_2} = [(x+y, x-y)]_{{\cal B}_2}
= x (1,1) + y (1,-1) = \begin{bmatrix}x \\ y \end{bmatrix}, \;
{\mbox{ and }}$](img1844.png)
![$\displaystyle T[{\cal B}_1, {\cal B}_2] \; [(x,y)]_{{\cal B}_1} = \begin{bmatri...
...d{bmatrix} =
\begin{bmatrix}x \\ y \end{bmatrix}=[T(\;(x,y) \;)]_{{\cal B}_2}.$](img1845.png)
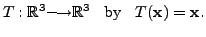
Then
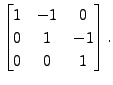 |
![$ T[{\cal B}_1, {\cal B}_1] =
\begin{bmatrix}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1
\end{bmatrix}.$](img1858.png)
![$\displaystyle T[{\cal B}_1, {\cal B}_2] = \begin{bmatrix}1 & 1 & -1 \\ 1 & 0 & 1 \end{bmatrix}.$](img1863.png)
Check that that
Find the matrix of the linear transformation
However, note that the image of the linear transformation is contained
in
![]()
That is, we multiply the matrix of the linear transformation with the coordinates
We sometimes write
A K Lal 2007-09-12