Next: Inner Product Spaces Up: Linear Transformations Previous: Rank-Nullity Theorem Contents
In the last few sections, the following has been discussed in detail:
Given a finite dimensional vector space ![]() of dimension
of dimension ![]() we fixed an ordered basis
we fixed an ordered basis ![]() For any
For any
![]() we calculated the column vector
we calculated the column vector
![]() to obtain the
coordinates of
to obtain the
coordinates of
![]() with respect to the ordered basis
with respect to the ordered basis ![]() Also,
for any linear transformation
Also,
for any linear transformation
![]() we got an
we got an
![]() matrix
matrix
![]() the matrix of
the matrix of ![]() with respect to the ordered basis
with respect to the ordered basis ![]() That is, once an ordered basis of
That is, once an ordered basis of ![]() is fixed,
every linear transformation is represented by a matrix with
entries from the scalars.
is fixed,
every linear transformation is represented by a matrix with
entries from the scalars.
In this section, we understand the matrix
representation of ![]() in terms of different
bases
in terms of different
bases
![]() and
and
![]() of
of ![]() That is, we relate the two
That is, we relate the two
![]() matrices
matrices
![]() and
and
![]() We start with the following important theorem.
This theorem also enables us to understand WHY THE MATRIX PRODUCT
IS DEFINED SOMEWHAT DIFFERENTLY.
We start with the following important theorem.
This theorem also enables us to understand WHY THE MATRIX PRODUCT
IS DEFINED SOMEWHAT DIFFERENTLY.
Now for
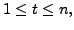
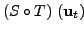 |
![$\displaystyle S ( T({\mathbf u}_t) ) = S \biggl( \sum\limits_{j=1}^m (T[{\cal B...
...\biggr) = \sum\limits_{j=1}^m
(T[{\cal B}_1, {\cal B}_2])_{jt} S({\mathbf v}_j)$](img2048.png) |
||
![$\displaystyle \sum\limits_{j=1}^m (T[{\cal B}_1,
{\cal B}_2])_{jt} \sum\limits_{k=1}^p (S[{\cal B}_2, {\cal B}_3])_{kj} {\mathbf w}_k$](img2049.png) |
|||
![$\displaystyle \sum\limits_{k=1}^p (\sum\limits_{j=1}^m (S[{\cal B}_2, {\cal B}_3])_{kj} (T[{\cal B}_1,
{\cal B}_2])_{jt}) {\mathbf w}_k$](img2050.png) |
|||
![$\displaystyle \sum\limits_{k=1}^p ( S[{\cal B}_2,
{\cal B}_3] \;\; T[{\cal B}_1, {\cal B}_2])_{kt} {\mathbf w}_k.$](img2051.png) |
Hence,
This completes the proof. height6pt width 6pt depth 0pt
Suppose
![]() Then using the rank-nullity theorem, observe that
Then using the rank-nullity theorem, observe that
So, to complete the proof of the second inequality, we need to show that
We now prove the first inequality.
Let
![]() and let
and let
![]() be a basis of
be a basis of
![]() Clearly,
Clearly,
![]() as
as
![]() We extend it to get a basis
We extend it to get a basis
![]() of
of
![]()
Claim: The set
![]() is linearly
independent subset of
is linearly
independent subset of
![]()
As
![]() the set
the set
![]() is a subset of
is a subset of
![]() Let if possible the given set be linearly dependent. Then there exist
non-zero scalars
Let if possible the given set be linearly dependent. Then there exist
non-zero scalars
 such that
such that
So, the vector
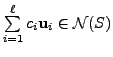 and is a
linear combination of the basis vectors
and is a
linear combination of the basis vectors
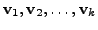 of
of
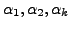 such that
such that
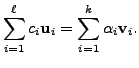
Or equivalently
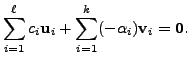
That is, the
Thus, the set
![]() is a
linearly independent subset of
is a
linearly independent subset of
![]() and so
and so
![]() Hence,
Hence,
height6pt width 6pt depth 0pt
Recall from Theorem 4.1.8 that if ![]() is an invertible
linear Transformation, then
is an invertible
linear Transformation, then
![]() is a linear transformation
defined by
is a linear transformation
defined by
![]() whenever
whenever
![]() We now state an important result about inverse of a linear transformation.
The reader is required to supply the proof (use Theorem
4.4.1).
We now state an important result about inverse of a linear transformation.
The reader is required to supply the proof (use Theorem
4.4.1).
![$\displaystyle T[{\cal B}_1, {\cal B}_2]^{-1} = T^{-1}[{\cal B}_2, {\cal B}_1].$](img2083.png)
Prove that
Let ![]() be a vector space with
be a vector space with
![]() Let
Let
![]() and
and
![]() be two
ordered bases of
be two
ordered bases of ![]() Recall from Definition 4.1.5
that
Recall from Definition 4.1.5
that
![]() is the identity linear
transformation defined by
is the identity linear
transformation defined by
![]() for every
for every
![]() Suppose
Suppose
![]() with
with
![$ [{\mathbf x}]_{{\cal B}_1} = (\alpha_1, \alpha_2, \ldots,
\alpha_n)^t$](img2097.png) and
and
![$ [{\mathbf x}]_{{\cal B}_2} = (\beta_1, \beta_2, \ldots,
\beta_n)^t.$](img2098.png)
We now express each vector in
![]() as a linear
combination of the vectors from
as a linear
combination of the vectors from
![]() Since
Since
![]() for
for
![]() and
and
![]() is a basis of
is a basis of ![]() we can find scalars
we can find scalars
![]() such that
such that
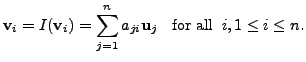
Hence,
![$ [I({\mathbf v}_i)]_{{\cal B}_1} = [{\mathbf v}_i]_{{\cal B}_1} = ( a_{1i}, a_{2i},
\cdots, a_{ni} )^t$](img2102.png) and
and  |
Equivalently,
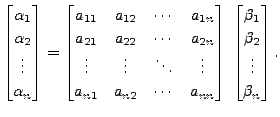
Note: Observe that the identity linear transformation
![]() defined by
defined by
![]() for every
for every
![]() is invertible and
is invertible and
![$\displaystyle I[{\cal B}_2, {\cal B}_1]^{-1} = I^{-1}[{\cal B}_1, {\cal B}_2]= I[{\cal B}_1, {\cal B}_2].$](img2110.png)
Therefore, we also have
Let ![]() be a finite dimensional vector space and let
be a finite dimensional vector space and let
![]() and
and
![]() be two ordered bases of
be two ordered bases of ![]() Let
Let
![]() be a linear transformation.
We are now in a position to relate the two matrices
be a linear transformation.
We are now in a position to relate the two matrices
![]() and
and
![]()
Also, let
![]() be the matrix of the identity
linear transformation with respect to the bases
be the matrix of the identity
linear transformation with respect to the bases
![]() and
and
![]() Then
Then
![]() Equivalently
Equivalently
![]()
Since the result is true for all
Another Proof:
Let
![]() and
and
![]() Then
for
Then
for
![]()
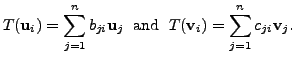
So, for each
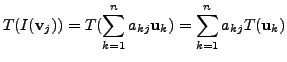 |
|||
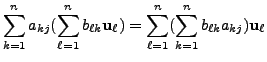 |
![$\displaystyle [T({\mathbf v}_j)]_{{\cal B}_1} = \begin{bmatrix}\sum\limits_{k=1...
...matrix} = B
\begin{bmatrix}a_{1j} \\ a_{2j} \\ \vdots \\ a_{nj} \end{bmatrix}.$](img2133.png)
Hence
Also, for each
![]()
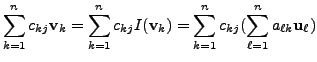 |
|||
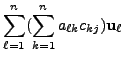 |
![$\displaystyle [T({\mathbf v}_j)]_{{\cal B}_1} = \begin{bmatrix}\sum\limits_{k=1...
...matrix} = A
\begin{bmatrix}c_{1j} \\ c_{2j} \\ \vdots \\ c_{nj} \end{bmatrix}.$](img2137.png)
This gives us
Let ![]() be a vector space with
be a vector space with
![]() and let
and let
![]() be
a linear transformation. Then for each ordered basis
be
a linear transformation. Then for each ordered basis ![]() of
of ![]() we get
an
we get
an
![]() matrix
matrix
![]() Also, we know that for
any vector space we have infinite number of choices for an ordered basis.
So, as we change an ordered basis, the matrix of the linear transformation
changes. Theorem 4.4.6 tells us that all these matrices are
related.
Also, we know that for
any vector space we have infinite number of choices for an ordered basis.
So, as we change an ordered basis, the matrix of the linear transformation
changes. Theorem 4.4.6 tells us that all these matrices are
related.
Now, let ![]() and
and ![]() be two
be two
![]() matrices such
that
matrices such
that
![]() for some invertible matrix
for some invertible matrix ![]() Recall the
linear transformation
Recall the
linear transformation
![]() defined by
defined by
![]() for all
for all
![]() Then we have seen that
if the standard basis of
Then we have seen that
if the standard basis of
![]() is the ordered basis
is the ordered basis ![]() then
then
![]() Since
Since ![]() is an invertible matrix, its columns
are linearly independent and hence we can take its columns as an ordered
basis
is an invertible matrix, its columns
are linearly independent and hence we can take its columns as an ordered
basis
![]() Then note that
Then note that
![]() The above observations
lead to the following remark and the definition.
The above observations
lead to the following remark and the definition.
is the set of all matrices that are similar to the given matrix
Then
![$\displaystyle [1+2x+x^2]_{{\cal B}_1} = (-1) \cdot 1 +
1 \cdot (1+x) + 1 \cdot (1+x+x^2) = (-1,1,1)^t, \; {\mbox{ and}}$](img2157.png)
Therefore,
![$\displaystyle [ [I(1 + x - x^2)]_{{\cal B}_1}, [I(1 + 2x + x^2)]_{{\cal B}_1},
[I(2 + x + x^2)]_{{\cal B}_1} ]$](img2159.png) |
|||
![$\displaystyle [ [1 + x - x^2]_{{\cal B}_1},
[1+ 2x + x^2]_{{\cal B}_1}, [2 + x + x^2]_{{\cal B}_1} ]$](img2160.png) |
|||
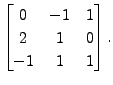 |
Then
![$\displaystyle T[{\cal B}_1, {\cal B}_1] =
\begin{bmatrix}0 & 0 & -2 \\ 1 & 1 &...
...}-{4/5} & 1 & {8/5} \\ -{2/5} & 2 & {9/5} \\ {8/5}
& 0 & -{1/5} \end{bmatrix}.$](img2167.png)
Find
Check that,
![$\displaystyle T[{\cal B}_1, {\cal B}_1] \; I[{\cal B}_2, {\cal B}_1] = I[{\cal ...
... B}_2] =
\begin{bmatrix}2 & -2 & -2 \\ -2 & 4 & 5 \\ 2 & 1 & 0
\end{bmatrix}.$](img2168.png)
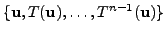
is a basis of
![$\displaystyle T[{\cal B}, {\cal B}] = \begin{bmatrix}0 & 0 & 0 & \cdots & 0 \\ ...
...ots & & \ddots & \ddots &
\vdots \\ 0 & 0 & \cdots & 1 & 0 \\
\end{bmatrix}.$](img2173.png)
Let
Let
A K Lal 2007-09-12