Next: Matrices over Complex Numbers Up: Matrices Previous: Block Matrices Contents
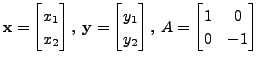 and
and
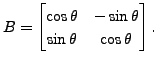 Geometrically interpret
Geometrically interpret
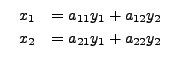 and
and
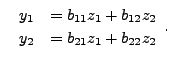
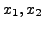 in terms of
in terms of 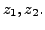
![$ {\mathbf x}^t = [ x_1, \;x_2 ], \; {\mathbf y}^t = [ y_1, \;y_2 ]$](img252.png) and
and
![$ {\mathbf z}^t = [ z_1, \;z_2]$](img253.png) then find matrices
then find matrices
Then for two square matrices,
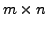 matrices and let
matrices and let
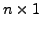 column vector.
column vector.
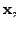 then
then 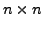 matrix such that
matrix such that 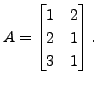 Show that there exist infinitely
many matrices
Show that there exist infinitely
many matrices ![$ A = \left[\begin{array}{cc\vert cc} 1 & 0 & 0 & 1 \\
0 & 1 & 1 & 1 \\
\hline 0 & 1 & 1 & 0 \\ 0 & 1 & 0 & 1 \end{array} \right]$](img276.png) and
and
![$ B =
\left[\begin{array}{cc\vert cc} 1 & 2 & 2 & 1 \\ 1 & 1 & 2 & 1 \\
\hline 1 & 1 & 1 & 1 \\ -1 & 1 & -1 & 1 \end{array} \right].$](img277.png)
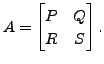 If
If 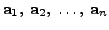 are the rows of
are the rows of 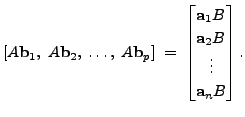 |
A K Lal 2007-09-12